Cho hình 51: Chứng minh ba điểm B, C, D thẳng hàng.
PB
Những câu hỏi liên quan
Cho hình 51 :
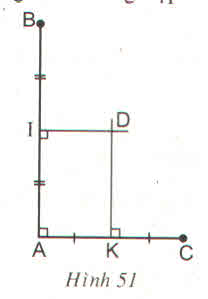
Chứng minh ba điểm B, C, D thẳng hàng
Gợi ý : Chứng minh \(\widehat{ADB}+\widehat{ADC}=180^0\)
Hướng dẫn:
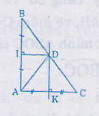
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800
Đúng 0
Bình luận (0)
Từ hình vẽ ta có:
DK là trung trực của Ac, DI là đường trung trực của AB. Do đó ∆ADK = ∆CDK (c.c.c)
=> ˆADK=ˆCDKADK^=CDK^
hay DK là phân giác ˆADCADC^
=> ˆADKADK^ = 1212ˆADCADC^
∆ADI = ∆BDI (c.c.c)
=> ˆADI=ˆBDIADI^=BDI^
=> DI là phân giác ˆADBADB^
=> ˆADIADI^ = 1212 ˆADBADB^
Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC
=> DK ⊥ DI
hay ˆADKADK^ + ˆADIADI^ = 900
Do đó 1212ˆADCADC^ + 1212 ˆADBADB^ = 900
=> ˆADCADC^ + ˆADBADB^ = 1800
Đúng 0
Bình luận (0)
Cho hình 88.
Chứng minh rằng BC // OO’ và ba điểm C, B, D thẳng hàng.
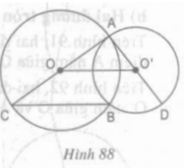
Xét tam giác ABC có:
OA = OB = OC = bán kính đường tròn (O)
Mà BO là trung tuyến của tam giác ABC
⇒ ∆ABC vuông tại B ⇒ AB ⊥ BC (1)
Lại có OO’ là đường trung trực của AB
⇒ AB ⊥ OO' (2)
Từ (1) và (2) ⇒ OO’ // BC
Chứng minh tương tự ta có ∆ABD vuông tại B ⇒ AB ⊥ BD (3)
Từ (1) và (3) ⇒ B, C, D thẳng hàng.
Đúng 0
Bình luận (0)
vẽ năm điểm : A , B , C , D , E sao cho ba điểm A , B , C thẳng hàng ba điêm B , C , D thẳng hàng , ba điểm C,D,E không thẳng hàng . Chứng minh bốn điểm A,B,C,D thẳng hàng
1.cho hình bình hành ABCD trên tia đối của AD lấy điểm E sao cho AE=AD .Gọi F là giao điểm của EC VÀ AB a) Chứng minh F là trung điểm của EC b) Chứng minh EBCA là hình binh hành c) Trên tia đối của CD lấy điểm T sao cho TC=CD.Chứng minh ba điểm T,B,E thẳng hàng d) Gọi giao của TA và EC là O. Chứng minh ba điểm D,O,B thẳng hàng
GIÚP MK VS, MK ĐANG CẦN GẤP Ạ
Câu thứ nhất sai đề bạn ạ vì ko có tia đối của tia AD
Chứng minh rằng ba điểm C, B, D ở hình dưới thẳng hàng.
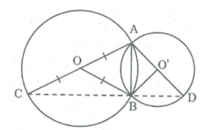
Nối AB, BO, BC, BO', BD.
* Trong ∆ ABC, ta có: OA = OC = R (bán kính đường tròn (O))
Nên BO là đường trung tuyến của ∆ ABC.
Mà BO = R (bán kính (O)) ⇒ BO = OA= OC = 1/2 AC
Suy ra tam giác ABC vuông tại B ⇒ ∠ (ABC) = 90 0
* Trong ∆ ABD , ta có: AO' = O'D = R' (bán kính đường tròn (O'))
Nên BO' là đường trung tuyến của tam giác ABD.
Mà BO' = R' (bán kính (O')) ⇒ BO' = AO' = O'D = 1/2 AD
Suy ra tam giác ABD vuông tại B ⇒ ∠ (ABD) = 90 0
Ta có: ∠ (ABC) + ∠ (ABD) = ∠ (CBD) = 90 0 + 90 0 = 180 0
Vậy C, B, D thẳng hàng.
Đúng 0
Bình luận (0)
Cho 4 điểm A,B,C,D trong đó A,B,C,D thẳng hàng, ba điểm B,C,D thẳng hàng. Chứng minh A,B,C,D thẳng hàng
Vì đầu bài nói A,B,C,D thẳng hàng
Đúng 0
Bình luận (0)
Cho hình vẽ Chứng minh ba điểm B K C thẳng hàng
Xem thêm câu trả lời
Cho hình dưới (hình 65a). Chứng minh rằng ba điểm B, K, C thẳng hàng
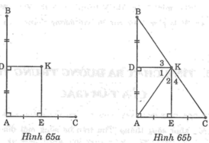
Nối KA, KB, KC (hình 65b).
Vì KD là đường trung trực của AB nên:
KA = KB (tính chất đường trung trực)
Suy ra: ΔKAB cân tại K
Do đó KD là đường phân giác của ∠(AKB)
Suy ra: ∠K1 = ∠K3 ⇒ ∠(AKB) = 2 ∠K1 (1)
Vì KE là đường trung trực của AC nên:
KA = KC (tính chất đường trung trực)
Do đó, tam giác AKC cân tại K. Suy ra KE là đường phân giác của ∠(AKC)
Suy ra: ∠K2 = ∠K4 ⇒ ∠(AKC) = 2 ∠K2 (2)
Ta có: KD ⊥ AB (gt) và AC ⊥ AB (gt)
Suy ra: KD // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song nhau)
Lại có: KE ⊥ AC (gt)
Suy ra: KE ⊥ KD (quan hệ giữa tính vuông góc và tính song song)
Hay: ∠(DKE) = 90o⇒ ∠K1 +∠K2 = 90o
Từ (1) và (2) suy ra: ∠(AKB) + ∠(AKC) = 2∠K1 + 2∠K2
= 2.( ∠K1 +∠K2 ) = 2.90o = 180o.
Vậy B, K, C thẳng hàng.
Đúng 0
Bình luận (0)
Cho hai hình vuông ABCD và DEFG, trong đó các bộ ba điểm A, D, G và D, C, E sắp xếp theo thứ tự thẳng hàng. Trên tia AD lấy điểm H sao cho AHDG, trên tia CE lấy điểm K sao cho CKDG.a) Chứng minh bốn tam giác ABH, HGF, FEK, BCK bằng nhau.b) Chứng minh BHFK là hình vuông.c) Gọi J là tâm đối xứng của hình vuông BHFK. Chứng minh ba điểm A, C, J thẳng hàng. d) Chứng minh ba đường thẳng AC, GE, HK đồng qui.
Đọc tiếp
Cho hai hình vuông ABCD và DEFG, trong đó các bộ ba điểm A, D, G và D, C, E sắp xếp theo thứ tự thẳng hàng. Trên tia AD lấy điểm H sao cho AH=DG, trên tia CE lấy điểm K sao cho CK=DG.
a) Chứng minh bốn tam giác ABH, HGF, FEK, BCK bằng nhau.
b) Chứng minh BHFK là hình vuông.
c) Gọi J là tâm đối xứng của hình vuông BHFK. Chứng minh ba điểm A, C, J thẳng hàng.
d) Chứng minh ba đường thẳng AC, GE, HK đồng qui.