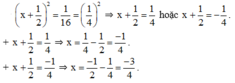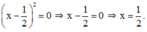1/2 nha bạn chọn đúng giúp mình

ta có (x+1)(x-2) <0 suy ra x+1 <0 đồng thời x-2<0 suy ra x <-1 và x< 2 chọn x<2. 
Kết luận x<2

\(x^2+\frac{1}{x^2}+y^2+\frac{1}{y^2}=4\)

\(\Leftrightarrow x^2-2\cdot x\cdot\frac{1}{x}+\frac{1}{x^2}+y^2-2\cdot y\cdot\frac{1}{y}+\frac{1}{y^2}=0\)

\(\Leftrightarrow\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2=0\)

\(\Leftrightarrow\hept{\begin{cases}x-\frac{1}{x}=0\\y-\frac{1}{y}=0\end{cases}\Leftrightarrow\hept{\begin{cases}\orbr{\begin{cases}x=-1\\x=1\end{cases}}\\\orbr{\begin{cases}y=-1\\y=1\end{cases}}\end{cases}}}\)\(\Leftrightarrow\hept{\begin{cases}x-\frac{1}{x}=0\\y-\frac{1}{y}=0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}\orbr{\begin{cases}x=-1\\x=1\end{cases}}\\\orbr{\begin{cases}y=1\\y=-1\end{cases}}\end{cases}}\)\(x-\frac{1}{x}=0\Leftrightarrow\orbr{\begin{cases}x=-1\\x=1\end{cases}}\)

\(y-\frac{1}{y}=0\Leftrightarrow\orbr{\begin{cases}y=1\\y=-1\end{cases}}\)

\(\left(x-2\right)\left(x+1\right)\le0\)

\(\Leftrightarrow\hept{\begin{cases}x-2\le0\\x+1\ge0\end{cases}}\) hoặc  \(\hept{\begin{cases}x-2\ge0\\x+1\le0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x\le2\\x\ge-1\end{cases}}\)   hoặc    \(\hept{\begin{cases}x\ge2\\x\le-1\end{cases}}\)

\(\Leftrightarrow-1\le x\le2\) hoặc  \(2\le x\le-1\) (loại)

Vậy \(-1\le x\le2\)

=> \(\left(x^2-2+\frac{1}{x^2}\right)+\left(y^2-2+\frac{1}{y^2}\right)=0\)

=> \(\left(x^2-2x.\frac{1}{x}+\frac{1}{x^2}\right)+\left(y^2-2.y.\frac{1}{y}+\frac{1}{y^2}\right)=0\)

=> \(\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2=0\)

<=> \(x-\frac{1}{x}=0;y-\frac{1}{y}=0\)

=> \(x^2=1;y^2=1\)

=> x = 1 hoặc -1

y = 1 hoặc -1

            \(x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}=4\)

\(\Leftrightarrow\)\(\left(x^2+\frac{1}{x^2}-2\right)+\left(y^2+\frac{1}{y^2}-2\right)=0\)

\(\Leftrightarrow\)\(\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2=0\)

\(\Leftrightarrow\)\(\hept{\begin{cases}x-\frac{1}{x}=0\\y-\frac{1}{y}=0\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x^2=1\\y^2=1\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x=\pm1\\y=\pm1\end{cases}}\)

\(^{x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}=4}\)

\(\Leftrightarrow\left(x^2+\frac{1}{x^2}\right)+\left(y^2+\frac{1}{y^2}\right)-2-2=0\)

\(\Leftrightarrow\left(x^2-2.x.\frac{1}{x}+\frac{1}{x^2}\right)+\left(y^2-2.y.\frac{1}{y}+\frac{1}{y^2}\right)=0\)

\(\Leftrightarrow\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2=0\)

Mặt khác:  \(\left(x-\frac{1}{x}\right)^2\ge0\)\(\forall\)x\(\ne\)0

                  \(\left(y-\frac{1}{y}\right)^2\ge0\)\(\forall\)y \(\ne\)0

Từ hai điều trên \(\Rightarrow\)\(\left(x-\frac{1}{x}\right)^2+\left(y-\frac{1}{y}\right)^2\ge0\)\(\forall\)x,y \(\ne\)0

Dấu "=" xảy ra 

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}\left(x-\frac{1}{x}\right)^2=0\\\left(y-\frac{1}{y}\right)^2=0\end{cases}}\)

                         \(\Leftrightarrow\hept{\begin{cases}x-\frac{1}{x}=0\\y-\frac{1}{y}=0\end{cases}}\)

                          \(\Leftrightarrow\hept{\begin{cases}x^2-1=0\\y^2-1=0\end{cases}}\)(vì x,y khác 0)

                          \(\Leftrightarrow\hept{\begin{cases}x^2=1\\y^2=1\end{cases}}\)

                           \(\Leftrightarrow\hept{\begin{cases}x=\pm1\\y=\pm1\end{cases}}\)

Vậy.....