Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau: 9 a 2 b 2 + 4 - 4 b t ạ i a = - 2 , b = - 3
PB
Những câu hỏi liên quan
Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau:
4
4
1
+
6
x
+
9
x
2
2
t
ạ
i
x
-...
Đọc tiếp
Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau: 4 4 1 + 6 x + 9 x 2 2 t ạ i x = - 2
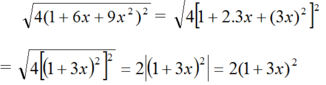
(vì (1 + 3x)2 > 0)
Thay x = √2 vào ta được:
2[1 + 3.(-√2)]2 = 2(1 - 3√2)2
= 2(1 - 6√2 + 32.2) = 2 - 12√2 + 36
= 38 - 12√2 = 38 - 12.1,414 = 38 - 16,968
= 21,032
Đúng 0
Bình luận (0)
Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau:
a
)
4
1
+
6
x
+
9
x
2
2
t
ạ
i
x
...
Đọc tiếp
Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau:
a ) 4 1 + 6 x + 9 x 2 2 t ạ i x = - 2 b ) 9 a 2 b 2 + 4 - 4 b t ạ i a = - 2 ; b = - 3
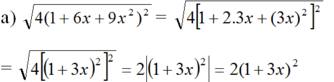
(vì (1 + 3x)2 > 0)
Thay x = √2 vào ta được:
2[1 + 3.(-√2)]2 = 2(1 - 3√2)2
= 2(1 - 6√2 + 32.2) = 2 - 12√2 + 36
= 38 - 12√2 = 38 - 12.1,414 = 38 - 16,968
= 21,032
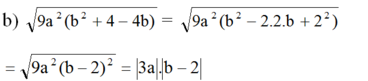
Thay a = -2, b = -√3 ta được:
|3(-2)|.|-√3 - 2| = 6(√3 + 2)
= 6(1,732 + 2) = 6.3,732
= 22,392
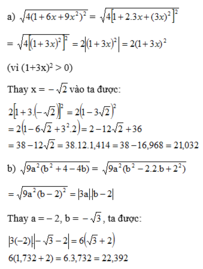
Đúng 0
Bình luận (0)
Bài 24 (trang 15 SGK Toán 9 Tập 1)
Rút gọn và tìm giá trị (làm tròn đến chữ số thập phân thứ ba) của các căn thức sau:
a) $\sqrt{4(1+6x+9x^2)^2}$ tại $x=−\sqrt{2}$ ;
b) $\sqrt{9a^2(b^2+4−4b)}$ tại $a=−2;b=−\sqrt{3}$.
a) Ta có:
√4(1+6x+9x2)24(1+6x+9x2)2 =√4.√(1+6x+9x2)2=4.(1+6x+9x2)2
=√4.√(1+2.3x+32.x2)2=4.(1+2.3x+32.x2)2
=√22.√[12+2.3x+(3x)2]2=22.[12+2.3x+(3x)2]2
=2.√[(1+3x)2]2=2.[(1+3x)2]2
=2.∣∣(1+3x)2∣∣=2.|(1+3x)2|
=2(1+3x)2=2(1+3x)2.
(Vì (1+3x)2>0(1+3x)2>0 với mọi xx nên ∣∣(1+3x)2∣∣=(1+3x)2|(1+3x)2|=(1+3x)2)
Thay x=−√2x=−2 vào biểu thức rút gọn trên, ta được:
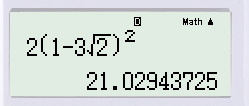
2[1+3.(−√2)]2=2(1−3√2)22[1+3.(−2)]2=2(1−32)2.
Bấm máy tính, ta được: 2(1−3√2)2≈21,0292(1−32)2≈21,029.
b) Ta có:
√9a2(b2+4−4b)=√32.a2.(b2−4b+4)9a2(b2+4−4b)=32.a2.(b2−4b+4)
=√(3a)2.(b2−2.b.2+22)=(3a)2.(b2−2.b.2+22)
=√(3a)2.√(b−2)2=(3a)2.(b−2)2
=|3a|.|b−2|=|3a|.|b−2|
Thay a=−2a=−2 và b=−√3b=−3 vào biểu thức rút gọn trên, ta được:
|3.(−2)|.∣∣−√3−2∣∣=|−6|.∣∣−(√3+2)∣∣|3.(−2)|.|−3−2|=|−6|.|−(3+2)|
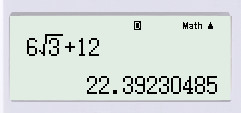
=6.(√3+2)=6√3+12=6.(3+2)=63+12.
Bấm máy tính, ta được: 6√3+12≈22,39263+12≈22,392.
a) x = 21 , 029
b) x = 22 , 392
Xem thêm câu trả lời
Rút gọn và tìm giá trị ( làm tròn đến chữ số thập phân thứ ba) của các căn thức sau:
a. \(\sqrt{4\left(1+6x+9x^2\right)^2}\) tại x = \(-\sqrt{2}\)
b. \(\sqrt{9a^2\left(b^2+4-4b\right)}\) tại a= -2; b= \(-\sqrt{3}\)
Đaq cần gấp, m.n giúp mk nka
a) \(\sqrt{4\left(1+6x+9x^2\right)^2}\) = \(\sqrt{\left(2\left(1+6x+9x^2\right)\right)^2}\)
= \(\sqrt{\left(2\left(1-6\sqrt{2}+18\right)\right)^2}\) = \(2\left(1-6\sqrt{2}+18\right)\) = \(2\left(3\sqrt{2}-1\right)^2\)
= \(21,029\)
b) \(\sqrt{9a^2\left(b^2+4-4b\right)}\) = \(\sqrt{\left(3a\left(b-2\right)\right)^2}\) = \(\sqrt{\left(-6\left(-\sqrt{3}-2\right)\right)^2}\)
= \(\sqrt{\left(6\sqrt{3}+12\right)^2}\) = \(6\sqrt{3}+12\) = \(22,392\)
Đúng 0
Bình luận (0)
Rút gọn và tìm giá trị (làm tròn đền chữ số thập phân thứ ba) của các căn thức sau:
a. \(\sqrt{4\left(1+6x+9x^2\right)^2}\) tại \(x=-\sqrt{2};\)
b. \(\sqrt{9a^2\left(b^2+4-4b\right)}\) tại \(a=-2;b=-\sqrt{3}.\)
a) = √4.
= 2(1 + 6x+
).
Tại x = -√2, giá trị của là 2(1 + 6(-√2) + 9(
= 2(1 - 6√2 +9.2)
= 2(19 - 6√2) ≈ 21,03.
b) =
= √9..
= 3.│a│.│b - 2│.
Tại a = -2 và b = -√3, giá trị của biểu thức là 3.│-2│.│-√3 - 2│= 3.2.(√3 + 2) = 6(√3 + 2) ≈ 22,392.
Đúng 0
Bình luận (0)
a) = √4.
= 2(1 + 6x+
).
Tại x = -√2, giá trị của là 2(1 + 6(-√2) + 9(
= 2(1 - 6√2 +9.2)
= 2(19 - 6√2) ≈ 21,03.
b) =
= √9..
= 3.│a│.│b - 2│.
Tại a = -2 và b = -√3, giá trị của biểu thức là 3.│-2│.│-√3 - 2│= 3.2.(√3 + 2) = 6(√3 + 2) ≈ 22,392.
Đúng 0
Bình luận (0)
Tìm giá trị gần đúng của căn bậc ba mỗi số sau bằng bảng lập phương và kiểm tra bằng máy tính bỏ túi (làm tròn đến chữ số thập phân thứ ba): 25,3
Tìm giá trị gần đúng của căn bậc ba mỗi số sau bằng bảng lập phương và kiểm tra bằng máy tính bỏ túi (làm tròn đến chữ số thập phân thứ ba): -37,91
Tìm giá trị gần đúng của căn bậc ba mỗi số sau bằng bảng lập phương và kiểm tra bằng máy tính bỏ túi (làm tròn đến chữ số thập phân thứ ba): 12
Tìm giá trị gần đúng của căn bậc ba mỗi số sau bằng bảng lập phương và kiểm tra bằng máy tính bỏ túi (làm tròn đến chữ số thập phân thứ ba): -0,08


