a) Vẽ tam giác đều ABC cạnh a = 3cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).
PB
Những câu hỏi liên quan
a) Vẽ tam giác đều ABC cạnh a = 3 cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O ; R).
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).
Đúng 0
Bình luận (0)
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).
Đúng 1
Bình luận (0)
Cho tam giác đều ABC cạnh a. vẽ đường tròn (O) có đường kính là đường cao AH của tam giác.Gọi (I) là đường tròn nội tiếp tam giác ABC. Tính diện tích phần chung của tam giác ABC với đường tròn (O) nhưng không thuộc đường tròn (I).áp dụng với a=căn bậc hai của 11.
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng
Đọc tiếp
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng A.
4
π
a
3
3
27
B.
20
π...
Đọc tiếp
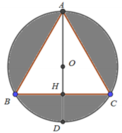
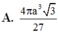
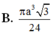
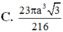
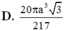
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng
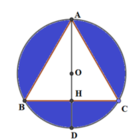
A. 4 π a 3 3 27
B. 20 π a 3 3 217
C. π a 3 3 24
D. 23 π a 3 3 216
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng A.
4
π
a
3
3
27
B.
π...
Đọc tiếp
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng
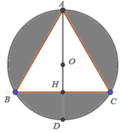
A. 4 π a 3 3 27
B. π a 3 3 24
C. 23 π a 3 3 216
D. 20 π a 3 3 217
Đáp án C
Phương pháp: Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng thể tích hình cầu đường kính AD trừ đi thể tích hình nón tạo bởi khi quay tam giác ABC quanh trục AD.
Cách giải:
*) Tính thể tích hình cầu đường kính AD:
Tam giác ABC đều, cạnh a
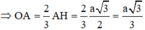
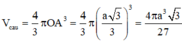
*) Tính thể tích hình nón (H) tạo bởi khi quay tam giác ABC quanh trục AH:
Hình nón (H) có đường cao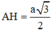 
, bán kính đáy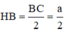 
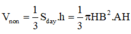
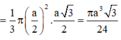
*) Tính V
Đúng 0
Bình luận (0)
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng A.
4
πa
3
3
27
B.
20
πa
3...
Đọc tiếp
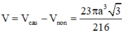
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh khi cho phần tô đậm (hình vẽ) quay quanh đường thẳng AD bằng
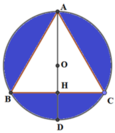
A. 4 πa 3 3 27
B. 20 πa 3 3 217
C. πa 3 3 24
D. 24 πa 3 3 216
Thể tích cần tìm bằng thể tích của khối cầu đường kính AD trừ đi thể tích khối nón sinh bởi tam giác ABC khi quay quanh trục AD.
+) ∆ A D C vuông tại C ⇒ a D = A C c o s D A C = a 3 2 = 2 a 3
⇒ Bán kính khối cầu đường kính AD là: R = a 3
⇒ V c a u = 4 3 π . a 3 3 = 4 πa 3 3 27
+) ∆ A B C đều cạnh a ⇒ A H = a 3 3 r = H B = H C = a 2
Thể tích khối nón là:
V n o n = 1 3 π ( a 2 ) 2 . a 3 2 = πa 3 3 24
Thể tích cần tìm là:
V = 4 πa 3 3 27 - πa 3 3 24 = 24 πa 3 3 216
Chọn đáp án D.
Đúng 0
Bình luận (0)
Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn (O) sao cho OA 2R. Từ A vẽ tiếp tuyến AB của đường tròn (O) (B là tiếp điểm).1) Chứng minh tam giác ABO vuông tại B và tính độ dài AB theo R (1đ)2) Từ B vẽ dây cung BC của (O) vuông góc với cạnh OA tại H. Chứng minh AC là tiếp tuyến của đường tròn (O). (1đ)3) Chứng minh tam giác ABC đều. (1đ)4) Từ H vẽ đường thẳng vuông góc với AB tại D. Đường tròn đường kính AC cắt cạnh DC tại E. Gọi F là trung điểm của cạnh OB. Chứng minh ba điểm A, E,...
Đọc tiếp
Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn (O) sao cho OA = 2R. Từ A vẽ tiếp tuyến AB của đường tròn (O) (B là tiếp điểm).
1) Chứng minh tam giác ABO vuông tại B và tính độ dài AB theo R (1đ)
2) Từ B vẽ dây cung BC của (O) vuông góc với cạnh OA tại H. Chứng minh AC là tiếp tuyến của đường tròn (O). (1đ)
3) Chứng minh tam giác ABC đều. (1đ)
4) Từ H vẽ đường thẳng vuông góc với AB tại D. Đường tròn đường kính AC cắt cạnh DC tại E. Gọi F là trung điểm của cạnh OB. Chứng minh ba điểm A, E, F thẳng hàng. (0.5đ)
123 làm được rồi help mình câu 4
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng
Đọc tiếp
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng A.
23
π
a
3
3
216
B.
π
a
3...
Đọc tiếp
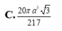
Cho tam giác ABC đều cạnh a và nội tiếp trong đường tròn tâm O, AD là đường kính của đường tròn tâm O. Thể tích của khối tròn xoay sinh ra khi cho phần màu vàng nhạt (hình vẽ bên dưới) quay quanh đường thẳng AD bằng
A. 23 π a 3 3 216
B. π a 3 3 24
C. 20 π a 3 3 217
D. 4 π a 3 3 27
