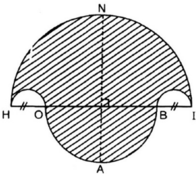
Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.
Hình 62
a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.
b) Tính diện tích hình HOABINH (miền gạch sọc).
c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .
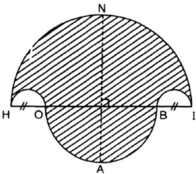
Hình 62
a) Cách vẽ
- Vẽ nửa đường tròn đường kính HI = 10cm, tâm M.
- Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.
- Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).
- Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.
b)
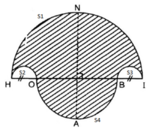
Diện tích miền gạch sọc bằng:
S = S 1 − S 2 − S 3 + S 4
với:
+ S 1 là nửa đường tròn đường kính HI
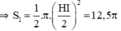
+ S 2 ; S 3 là nửa đường tròn đường kính HO và BI.
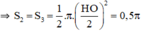
+ Ta tính OB:
Ta có: HO+ OB + BI = HI
⇔ 2+ OB + 2= 10 nên OB = 6
+ S4 là nửa đường tròn đường kính OB
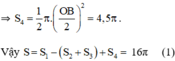
c)Ta có: 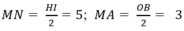
Do đó, NA = MN+ MA= 8
Diện tích hình tròn đường kính NA bằng : π 4 2 = 16 π ( c m 2 ) ( 2 )
so sánh (1) và (2) ta thấy hình tròn đường kính NA có cùng diện tích với hình HOABINH.
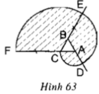
Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1cm. Nêu cách vẽ (h.63).
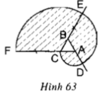
Cách vẽ
- Vẽ tam giác đều ABC cạnh 1cm. Dựa vào tính chất góc ngoài của tam giác ta có:
![]()
- Vẽ 1/3 đường tròn tâm A, bán kihs 1cm, ta được cung CD
- Vẽ 1/3 đường tròn tâm B, bán kính 2cm, ta được cung DE
- Vẽ 1/3 đường tròn tâm C, bán kính 3cm, ta được cung EF
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
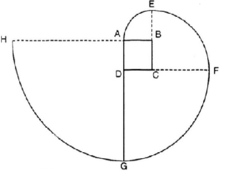
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
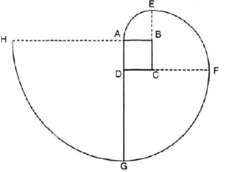
Hình 55
Cách vẽ:

Kiến thức áp dụng
+ Độ dài đường tròn đường kính d là: C = π.d
a) Vẽ lại hình tạo bởi các cung tròn xuất phát từ đỉnh C của tam giác đều ABC cạnh 1cm. Nêu cách vẽ (h.63).
b) Tính diện tích miền gạch sọc.

Kiến thức áp dụng
Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
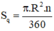
Vẽ lại ba hình (tạo bởi các cung tròn) dưới đây và tính chu vi mỗi hình (có gạch chéo):
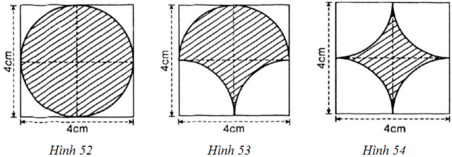
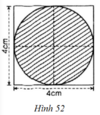
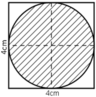
- Hình 52:
Phần gạch chéo là đường tròn đường kính d = 4cm
⇒ Chu vi của hình là: C = π.d = 4π ≈ 12,57 (cm)
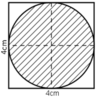
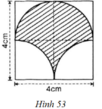
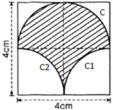
- Hình 53:
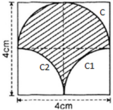
Chu vi gồm nửa đường tròn C; cung tròn C1 và cung tròn C2.
+ C là nửa đường tròn đường kính d = 4cm
⇒ C = π.d/2 = 2π (cm)
+ C1 và C2 là ¼ đường tròn bán kính R = 2cm
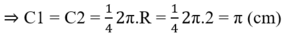
Vậy chu vi phần gạch chéo bằng:
C + C 1 + C 2 = 2 π + π + π = 4 π ≈ 12 , 57 ( c m )
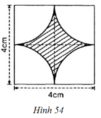
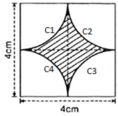
- Hình 54:
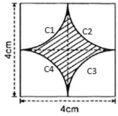
Chu vi cần tính là 4 cung tròn C 1 ; C 2 ; C 3 ; C 4 .
C 1 ; C 2 ; C 3 ; C 4 đều là ¼ đường tròn bán kính R = 2cm.
⇒ C 1 = C 2 = C 3 = C 4
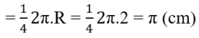
⇒ Chu vi phần hình gạch chéo:
C = C 1 + C 2 + C 3 + C 4 = 4 π ≈ 12 , 57 ( c m ) .
Kiến thức áp dụng
+ Độ dài đường tròn đường kính d là: C = π.d
Vẽ lại ba hình (tạo bởi các cung tròn) dưới đây và tính chu vi mỗi hình (có gạch chéo):
- Hình 52:
Phần gạch chéo là đường tròn đường kính d = 4cm
⇒ Chu vi của hình là: C = π.d = 4π ≈ 12,57 (cm)
- Hình 53:
Chu vi gồm nửa đường tròn C; cung tròn C1 và cung tròn C2.
+ C là nửa đường tròn đường kính d = 4cm
⇒ C = π.d/2 = 2π (cm)
+ C1 và C2 là ¼ đường tròn bán kính R = 2cm
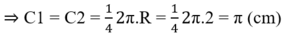
Vậy chu vi phần gạch chéo bằng:
C + C1 + C2 = 2π + π + π = 4π ≈ 12,57 (cm)
- Hình 54:
Chu vi cần tính là 4 cung tròn C1 ; C2; C3; C4.
C1 ; C2; C3; C4 đều là ¼ đường tròn bán kính R = 2cm.
⇒ C1 = C2 = C3 = C4
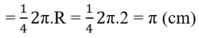
⇒ Chu vi phần hình gạch chéo:
C = C1 + C2 + C3 + C4 = 4π ≈ 12,57 (cm).
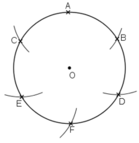
a) Vẽ đường tròn tâm O, bán kính R = 2cm. Nêu cách vẽ cung AB có số đo bằng 60o. Hỏi dây AB dài bao nhiêu xentimet?
b) Làm thế nào để chia được đường tròn thành sáu cung bằng nhau như trên hình 12?
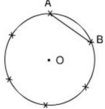
Hình 12
a) + Dùng compa vẽ đường tròn tâm O, bán kính R = 2cm.
+ Trên đường tròn lấy điểm A.Nối OA từ đó vẽ góc 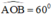
Khi đó ta được cung AB có số đo bằng 60 º .
+ ΔAOB có OA = OB,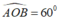
⇒ ΔAOB đều
⇒ AB = OA = OB = R = 2cm.
b) Chia đường tròn thành 6 cung bằng nhau:
+ Vẽ đường tròn tâm O, bán kính R.
+ Trên đường tròn tâm O, lấy điểm A.
+ Vẽ cung tròn tâm A, bán kính R cắt đường tròn tại B và C.
+ Vẽ cung tròn tâm B và C bán kính R cắt đường tròn tâm O tại giao điểm thứ hai là D và E.
+ Vẽ cung tròn tâm E bán kính R cắt đường tròn (O) tại giao điểm thứ hai là F.
Khi đó, ta chia được đường tròn thành sáu cung bằng nhau như trên
Cho đường tròn (7; 2cm). Vẽ bán kính IA và IB sao cho A I B ^ = 120 0 . Hãy tính:
a, Độ dài cung nhỏ AB
b, Diện tích hình quạt tròn giới hạn bởi cung nhỏ AB và hai bán kính IA, IB
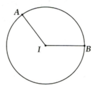
a, A I B ^ = 120 0 là góc tâm của (O; R) nên sđ A B ⏜ = 120 0
Áp dụng công thức tính độ dài cung tròn l = πRn 180 với R = 2cm; n 0 = 120 0
Độ dài cung nhỏ AB là: l = π . 2 . 120 180 = 4 π 3 cm
b, Diện tích hình quạt tròn giới hạn bởi cung nhỏ AB và hai bán kính IA, IB là phần tô màu xám
Áp dụng công thức: S = πR 2 n 360 với R = 2cm; n 0 = 120 0
Tính được S = 4 π 3 c m 2