Số đo góc 300 đổi sang rađian là:
![]()
![]()
![]()
![]()
Góc có số đo 1200 đổi sang rađian là góc
![]()
![]()
![]()
![]()
Chọn D.
Áp dụng công thức đổi độ ra rad ![]()
Do đó ![]()
Đổi số đo góc 1050 sang rađian bằng
![]()
![]()
![]()
![]()
Chọn B.
Áp dụng công thức đổi độ sang rad ![]()
Do đó 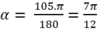
a) Đổi từ độ sang rađian các số đo sau: \({360^ \circ }, - {450^ \circ }\)
b) Đổi từ rađian sang độ các số đo sau: \(3\pi , - \frac{{11\pi }}{5}\)
a) Ta có:
\(\begin{array}{l}{360^ \circ } = 360.\frac{\pi }{{180}} = 2\pi \\ - {450^ \circ } = 450.\frac{\pi }{{180}} = \frac{5}{2}\pi \end{array}\)
b)\(3\pi = 3\pi .{\left( {\frac{{180}}{\pi }} \right)^ \circ } = {540^ \circ }\)
\( - \frac{{11\pi }}{5} = \left( { - \frac{{11\pi }}{5}} \right).{\left( {\frac{{180}}{\pi }} \right)^ \circ } = - {396^ \circ }\)
Số đo tính theo đơn vị rađian của góc 135 ° là:
A. 2 π 3
B. 3 π 4
C. 5 π 6
D. 6 π 7
Đáp án: B
Số đo tính theo đơn vị rađian của góc 135 ° là:
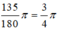
Đổi số đo của các cung sau ra rađian (chính xác đến 0,001): 137 ο
Đổi số đo của các cung sau ra rađian (chính xác đến 0,001): - 78 ο 35 '
Đổi số đo của các cung sau ra rađian (chính xác đến 0,001): 26 ο
Góc có số đo π 24 đổi sang độ là
A. 70
B.7030’
C.80 20’
D.80
Chọn B
Áp dụng công thức đổi rad sang độ 

Góc có số đo 2 π 5 đổi sang độ là
A. 240
B. 350
C. 720
D.270
Chọn C.
Áp dụng công thức đổi rad sang độ ![]()
Ta được số đo góc cần tính là: ![]()