Người ta trồng 3003 cây theo hình một tam giác như sau: hàng thứ nhất có 1 cây; hàng thứ 2 có 2 cây; hàng thứ 3 có 3 cây...hỏi có bao nhiêu hàng?
A. 76
B. 77
C. 78
D. 79
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Người ta trồng 3003 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây,...Hỏi có tất cả bao nhiêu hàng cây?
A. 73.
B. 75.
C. 77.
D. 79.
Chọn C.
Số cây mỗi hàng (bắt đầu từ hàng thứ nhất) lập thành một cấp số cộng có u1 = 1; d = 1
Giả sử có n hàng cây thì
Ta có 3003 = Sn = nu1 + ![]() ⇔ n2 + n – 6006 = 0 ⇔ n = 77.
⇔ n2 + n – 6006 = 0 ⇔ n = 77.
Người ta trồng 3003 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 2 cây, hàng thứ 3 trồng 3 cây, ..., hàng thứ k trồng k cây. Hỏi người ta đã trồng bao nhiêu hàng cây ?
A. 77
B. 78
C. 76
D. 75
Đáp án A
Đây là một dãy cấp số cộng với
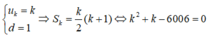
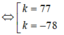
Người ta trồng 3003 cây theo dạng một hình tam giác như sau: hàng thứ nhất trồng 1 cây, hàng thứ hai trồng 2 cây, hàng thứ ba trồng 3 cây, ..., cứ tiếp tục trồng như thế cho đến khi hết số cây. Số hàng cây được trồng là
A. 77
B. 79
C. 76
D. 78
Người ta trồng 3003 cây theo hình tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ 2 có 2 cây, hàng thứ 3 có 3 cây,...Vậy có tất cả bao nhiêu hàng?
A. 75
B. 76
C. 77
D. 78
Chọn C
Tổng số cây trồng theo kiểu trên là
![]()
Người ta trồng 3003 cây theo hình tam giác như sau: hàng thứ nhất có 1 cây, hàng thứ hai có 2 cây, hàng thứ 3 có 3 cây,v.v....Hỏi có bao nhiêu hàng?
Ta gọi số hàng cây là: n
Thì ta có số cây sẽ là: 1 + 2 + 3 +...... n-1 + n = n(n+1)/2 (công thức n(n+1) hình như đã học rồi và đã đc chứng minh)
Nếu theo bạn nói thì ta sẽ có một công thức sau: n(n+1)/2 = 3003
<=> n² + n - 6006 = 0
=> n= 77 hoặc n= -78
Vậy ta chọn số hàng cây là 77
Gọi nn là số hàng cây. Khi đó số cây trên các hàng lần lượt là 1,2,3...,n
Theo giả thiết: 1+2+3+...+n=3003
⇔ n(n+1)2=3003
⇔ n2+n−6006=0
\(\Leftrightarrow\left[\begin{array}{nghiempt}n=-78\text{(loại)}\\n=77\left(TM\right)\end{array}\right.\)
Người ta trồng 3240 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ hàng thứ hai trở đi số cây trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi có tất cả bao nhiêu hàng cây ?
A. 81
B. 82
C. 80
D. 79
Người ta trồng 3240 cây theo một hình tam giác như sau: hàng thứ nhất trồng 1 cây, kể từ hàng thứ hai trở đi số cây trồng mỗi hàng nhiều hơn 1 cây so với hàng liền trước nó. Hỏi có tất cả bao nhiêu hàng cây ?
A. 81
B. 82
C. 80
D. 79
Người ta trồng cây theo hình tam giác, với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có 2 cây, ỏ hàng thứ 3 có 3 cây,… ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4950 cây. Hỏi số hàng cây được trồng theo cách trên là nbao nhiêu?
A. 101
B. 100
C. 99
D. 98
Đáp án C.
Phương pháp: Sử dụng tổng 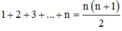
Cách giải: Giả sử trồng được n hàng cây với quy luật trên thì số cây trồng được là:
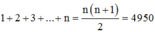
![]()
Người ta trồng cây theo hình tam giác với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có 2 cây, ở hàng thứ ba có 3 cây,... ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4950 cây. Hỏi số hàng cây được trồng theo cách trên là bao nhiêu?
A. 99
B. 100
C. 101
D. 98.