Tính đạo hàm của hàm số y = sin   2 x + cos   2 x 2 sin   2 x - cos   2 x

A. 

B. 

C.

D. 

Tính đạo hàm của hàm số: y = sin   x 1 + cos   x 3

A. 3 sin 2   x 1 + cos   x 3

B. 3 cos 2   x 1 + cos   x 3

C. - 3 sin 2   x 1 + cos   x 3

D. - 3 cos 2   x 1 + cos   x 3

Tính đạo hàm của hàm số sau  y = sin   x sin   x   -   cos   x

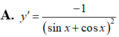
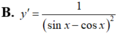
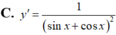
Tính đạo hàm của hàm số sau y   =   sin   x sin   x   -   cos   x

Cho hàm số y = x [ cos ( ln x ) + sin ( ln x ) ] . Khẳng định nào sau đây đúng