Cho hàm số y = e ax 2 + bx + c đạt cực trị tại x = 1 và đồ thị hàm số cắt trục tung tại điểm có tung độ bằng e 2 . Tính giá trị của hàm số tại x = 2
A. y 2 = 0
B. y 2 = e 2
C. y 2 = 1
D. y 2 = e
PB
Những câu hỏi liên quan
Cho hàm số yf(x)x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số yf(x) nào? A.
y
f
(
x
)
x
3
-
3
x
2
+
4
B.
y
f
(
x
)
x
3
+
6
x...
Đọc tiếp
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
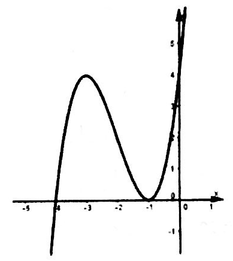
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
Tìm các hệ số a, b, ca,b,c của hàm số y=ax^2 + bx +cy=ax 2 +bx+c biết đồ thị của hàm số đó đi qua ba điểm A(1;-1)A(1;−1) , B(-2;-10)B(−2;−10) và C(0;-2)C(0;−2).
Xác định Parabol (P) : y = ax^2 + bx + c ( a khác 0 ) biết (P) đi qua :
a, điểm E (0; 6) và hàm số y = ax^2 - bx + c đạt giá trị nhỏ nhất là 4 khi x = -2
b, điểm F (1; 16) và cắt Ox tại các điểm có hoành độ là -1 và 5.
cho hàm số y=ax^2+bx+c
cmr f(-2).f(3) <= 0
Có phải mọi hàm số \(y=ax^2,y=ax^2+b\) và \(y=ax^2+bx+c\) đều là hàm số chẵn hay không?
cho hàm số y = ax^2 + bx + c(a khác 0). tìm a, b, c biết hàm số đó có gtln = 5 khi x = -2 và đồ thị đi qua M(1;-1)
\(y=ax^2+bx+c\left(d\right)\)
Do y có gtln là 5 khi x=-2
\(\Rightarrow\left\{{}\begin{matrix}5=a\left(-2\right)^2+b\left(-2\right)+c\\-\dfrac{b}{2a}=-2\\a< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4a-2b+c=5\\4a-b=0\end{matrix}\right.\)
Có \(M\in\left(d\right)\Rightarrow a+b+c=-1\)
Có hệ \(\left\{{}\begin{matrix}4a-2b+c=5\\4a+b=0\\a+b+c=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{-2}{3}\\b=-\dfrac{8}{3}\\c=\dfrac{7}{3}\end{matrix}\right.\)(tm)
Vậy...
Đúng 2
Bình luận (0)
cho y=ax^2+bx+c biết đồ thị của hàm số đó đi qua ba điểm A(2;4) B(−2;4) C(0;0).
\(\Leftrightarrow\left\{{}\begin{matrix}4a+2b+c=4\\4a-2b+c=4\\c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+b=2\\2a-b=2\\c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=0\\c=0\end{matrix}\right.\\ \Leftrightarrow y=x^2\)
Đúng 0
Bình luận (0)
a) Cho hàm số y=f(x)=ax5+bx3+cx-5 (a,b,c thuộc R)
Cho f(-3)=208. Tính f(3)=?
b) Cho hàm số y=g(x)=ax4-bx2+x+3 (a,b thuộc R)
Cho g(2)=17. Tính g(-2)=?
B1: Cho hàm số yfleft(xright)x^2+ax-a+5.Tìm a biết f(-2)2004B2: Cho hàm số yfleft(xright)ax+b.Tìm và b biết f(1)2 và f(2)3B3: Cho hàm số yfleft(xright)ax^2+bx+c.Tìm a,b,c biết f(o)1,f(1)2,f(2)3B4:Cho hàm số yx+1a,tìm tọa độ điểm A, biết A là giao điểm đồ thị với trục tungb, Tìm tọa độ điểm B biết B là giao điểm của đồ thị với trục hoànhB5: tìm tọa độ giao điểm của đồ thị hàm số y2x và y3x-1B6: Cho hàm số yax^2+bx+c tìm a,b,c biết đồ thị hàm số đi qua điểm A(0,1), B(1,2), C(-1,0)HELP ME!!!!!!!!!...
Đọc tiếp
B1: Cho hàm số \(y=f\left(x\right)=x^2+ax-a+5\).Tìm a biết f(-2)=2004
B2: Cho hàm số \(y=f\left(x\right)=ax+b.\)Tìm và b biết f(1)=2 và f(2)=3
B3: Cho hàm số \(y=f\left(x\right)=ax^2+bx+c.\)Tìm a,b,c biết f(o)=1,f(1)=2,f(2)=3
B4:Cho hàm số y=x+1
a,tìm tọa độ điểm A, biết A là giao điểm đồ thị với trục tung
b, Tìm tọa độ điểm B biết B là giao điểm của đồ thị với trục hoành
B5: tìm tọa độ giao điểm của đồ thị hàm số y=2x và y=3x-1
B6: Cho hàm số y=ax^2+bx+c tìm a,b,c biết đồ thị hàm số đi qua điểm A(0,1), B(1,2), C(-1,0)
HELP ME!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Giúp mình với ạ
CMR: Đồị của hàm số y= ax2 và đồ thị của hàm số y= ax2 +bx+c (a khác 0) tương tự nhau
Đặt (P) : y = ax2
(P') : y = ax2+bx+c
Ta có : (P') : \(y=ax^2+bx+c=a\left(x^2+\frac{2.x.b}{2a}+\frac{b^2}{4a^2}-\frac{b^2}{4a^2}\right)+c\)
\(=a\left(x+\frac{b}{2a}\right)^2+c-\frac{b^2}{4a}=a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a}\)
Đặt \(p=\frac{b}{2a}\) , \(q=-\frac{b^2-4ac}{4a}\) thì khi đó
\(\left(P'\right):y=a\left(x+p\right)^2+q\)
Điều này có nghĩa là ta tịnh tiến (P) sang phải p đơn vị , tịnh tiến lên trên q đơn vị thì được (P') => (P') thực chất là "phép tịnh tiến" của (P)
Từ đó bạn rút ra được điều phải chứng minh nhé!
Cách chứng minh trong SGK có viết rất rõ rồi , bạn tham khảo nhé !
Đúng 0
Bình luận (1)