Chứng minh rằng a < b ⇔ a – b < 0.
PB
Những câu hỏi liên quan
Bài 4: Chứng minh rằng: -(a-b-c)+(-a+b-c)-(-a+b+c)=-(a-b+c)
Bài 5: Cho M=(-a+b)-(b+c-a)+(c-a) Chứng minh rằng: Nếu a<0 thì M>0
Mình cần gấp ạ!
\(4,VT=-a+b+c-a+b-c+a-b-c=-a+b-c=-\left(a-b+c\right)=VP\\ 5,M=-a+b-b-c+a+c-a=-a\\ M>0\Rightarrow-a>0\Rightarrow a< 0\)
Đúng 5
Bình luận (0)
Cho a > b > c. Chứng minh rằng a / b < 2a / a + b
Cho 0 < a < b Chứng minh rằng a / b > 2a / a+b
1.a)Cho các số dương a,b,c có tích bằng 1.Chứng minh rằng (a+1)(b+1)(c+1) lớn hơn hoặc bằng 8.
b)Chocacs số a và b không âm.Chứng minh rằng (a+b)(ab+1) lớn hơn hoặc bằng 4ab.
2.Cho các số dương a,b,c,d có tích bằng 1.Chứng minh rằng a bình +b bình +c bình +d bình +ab+cd lớn hơn hoặc bằng 6.
3.Chứng minh rằng nếu a+b+c>0.abc>0.ab+bc+ca>0 thì a>0,b>0,c>0.
3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương.
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết
Vậy nên phải có ít nhất 1 số dương
Không mất tính tổng quát, giả sử a > 0
mà abc > 0 => bc > 0
Nếu b < 0, c < 0:
=> b + c < 0
Từ gt: a + b + c < 0
=> b + c > - a
=> (b + c)^2 < -a(b + c) (vì b + c < 0)
<=> b^2 + 2bc + c^2 < -ab - ac
<=> ab + bc + ca < -b^2 - bc - c^2
<=> ab + bc + ca < - (b^2 + bc + c^2)
ta có:
b^2 + c^2 >= 0
mà bc > 0 => b^2 + bc + c^2 > 0
=> - (b^2 + bc + c^2) < 0
=> ab + bc + ca < 0 (vô lý)
trái gt: ab + bc + ca > 0
Vậy b > 0 và c >0
=> cả 3 số a, b, c > 0
Đúng 0
Bình luận (0)
1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)
\(\left(b+c\right)^2\ge4b>0\)
\(\left(a+c\right)^2\ge4c>0\)
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)
Mà abc=1
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)
Đúng 0
Bình luận (0)
sai rồi. sửa a+b=a+1, b+c=b+1, a+c=c+1 nha, thông cảm, nhìn sai đề
Đúng 0
Bình luận (0)
a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: ![]()
b) Cho a, b, c > 0. Chứng minh rằng: ![]()
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = ab
\(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
Đúng 2
Bình luận (0)
Cho a > 0, b > 0. Chứng minh rằng a b + b a ≥ a + b
Cách 1: Sử dụng các phép biến đổi tương đương để chứng minh bất đẳng thức.
Ta có:

Do đó: 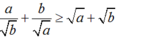 (đpcm)
(đpcm)
Cách 2: Sử dụng bất đẳng thức Cô-si để chứng minh bất đẳng thức.
Áp dụng bất đẳng thức Cô-si cho hai số dương 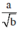 và √b ta có:
và √b ta có:

Dấu “=” xảy ra khi và chỉ khi a= b > 0
Đúng 0
Bình luận (0)
a) Cho a, b, c > 0. Chứng minh rằng M = \(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}\) không là số nguyên
b) Cho a, b, c thỏa mãn: a + b + c = 0. Chứng minh rằng ab + bc + ca nhỏ hơn hoặc bằng 0
Cho a # +b và a(a+b)(a+c)=b(b+c)(b+a). Chứng minh rằng a+b+c=0Cho a # +b và a(a+b)(a+c)=b(b+c)(b+a). Chứng minh rằng a+b+c=0
Chứng minh rằng, với a>b>0 thì a - b < a - b
Với a>b>0 để chứng minh a - b < a - b
ra quy về so sánh a v ớ i a - b + b
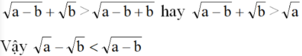
Đúng 0
Bình luận (0)
Chứng minh rằng, với a>b>0 thì a - b < a - b
Với a>b>0 để chứng minh a - b < a - b
ra quy về so sánh a v ớ i a - b + b
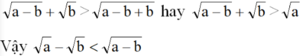
Đúng 0
Bình luận (0)