Hai lực thành phần F 1 v à F 2 có độ lớn lần lượt là F 1 v à F 2 , hợp lực F của chúng có độ lớn là F. Ta có:
A. F luôn lớn hơn F 1
B. F luôn nhỏ hơn F 2 .
C. F thỏa: | F 1 – F 2 | ≤ F ≤ F 1 + F 2 .
D. F không thể bằng F 1 .
HL
Những câu hỏi liên quan
Hai lực thành phần
F
1
→
và
F
2
→
có độ lớn lần lượt là F1 và F2, hợp lực
F
→
của chúng có độ lớn là F. Ta có: A. F luôn lớn hơn F1 B. F luôn nhỏ hơn F2 C. F thỏa mãn: D. F không thể bằng F1
Đọc tiếp
Hai lực thành phần F 1 → và F 2 → có độ lớn lần lượt là F1 và F2, hợp lực F → của chúng có độ lớn là F. Ta có:
A. F luôn lớn hơn F1
B. F luôn nhỏ hơn F2
C. F thỏa mãn: 
D. F không thể bằng F1
Chọn đáp án C
Quy tắc hình bình hành: Nếu hai lực đồng quy làm thành hai cạnh của một hình bình hành, thì đường chéo kẻ từ điểm đồng quy biểu diễn hợp lực của chúng:
Với:
F2 = F12 + F22 + 2F1F2cosa
Đúng 0
Bình luận (0)
Cho hai lực có độ lớn lần lượt là F1 = 8 N và F2 = 6 N. Độ lớn của hợp lực của chúng là F = 10 N. Góc giữa hai lực thành phần là
Cho hai lực đồng quy có độ lớn bằng 3N và 4N. Hỏi góc hợp bởi hai lực thành phần là bao nhiêu? Nếu hợp lực của hai lực trên có độ lớn là:
a) F= 5N. b) F = 6,47N.
Trong phép tổng hợp hai lực thì hai lực thành phần cùng với hợp lực tạo thành một hình tam giác. Độ lớn của các lực biểu diễn bằng độ dài của các cạnh tam giác đó.
Từ định lí hàm số cosin đối với tam giác, áp dụng cho trường hợp này ta có góc giữa hai lực đồng quy xác định bởi:
Đúng 0
Bình luận (0)
Phân tích lực F thành hai lực thành phần
F
1
và
F
2
vuông góc với nhau. Biết độ lớn của lực F 100 N;
F
1
60
N
thì độ lớn của lực
F
2
là A. 40 N. B. 80 N. C. 160 N. D. 640 N.
Đọc tiếp
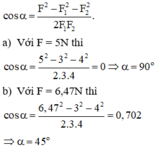
Phân tích lực F thành hai lực thành phần F 1 và F 2 vuông góc với nhau. Biết độ lớn của lực F = 100 N; F 1 = 60 N thì độ lớn của lực F 2 là
A. 40 N.
B. 80 N.
C. 160 N.
D. 640 N.
Đáp án B
F1 và F2 là hai lực vuông góc với nhau nên ta có:
Đúng 0
Bình luận (0)
Một vật nặng chịu tác dụng của 2 lực thành phần F1 và F2. Độ lớn của F1 = 200N. Lực F2 và hợp lực F lần lượt theo phương hợp với F1 60\(^o\) và 45\(^o\). Tính độ lớn lực F2 và độ lớn hợp lực F
Hai lực thành phần có độ lớn là F1=F2=b. F1 hợp với F2 một góc 90 độ. Biết rằng độ lớn hợp lực của hai lực trên là F = 14\(\sqrt{2}\). Xác định b.
Ta có: \(\overrightarrow{F_{hl}}=\overrightarrow{F_1}+\overrightarrow{F_2}\)
Lại có: \(\alpha=\left(\overrightarrow{F_1};\overrightarrow{F_2}\right)\)
\(F_1\)hợp với \(F_2\) một góc là \(90^o\).
\(F_{hl}=\sqrt{F_1^2+F_2^2+2F_1F_2cos\alpha}\) \(=\sqrt{b^2+b^2+2\cdot b\cdot b\cdot cos90^o}\) \(=\sqrt{2b^2+2b^2\cdot0}=\sqrt{2b^2}\)Mà \(F_{hl}=14\sqrt{2}N\)\(\Rightarrow\sqrt{2b^2}=14\sqrt{2}\)Bình phương hai vế ta đc: \(2b^2=\left(14\sqrt{2}\right)^2=392\)
\(\Rightarrow b^2=196\Rightarrow b=14N\)
Đúng 1
Bình luận (0)
Cho hai lực đồng quy có độ lớn
F
1
F
2
20
N
. Độ lớn của hợp lực là
F
34
,
6
N
khi hai lực thành phần hợp với nhau một góc là A.
60
o
B.
30
o
C. ...
Đọc tiếp
Cho hai lực đồng quy có độ lớn F 1 = F 2 = 20 N . Độ lớn của hợp lực là F = 34 , 6 N khi hai lực thành phần hợp với nhau một góc là
A. 60 o
B. 30 o
C. 90 o
D. 120 o
Phân tích vecto lực F thành lực vecto lực F1 và vecto lực F2 theo hai phương OA và OB (hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần? A. F1 F2 F B. F1 F2 F/2 C. F1 F2 1,15F D. F1 F2 0,58F
Đọc tiếp
Phân tích vecto lực F thành lực vecto lực F1 và vecto lực F2 theo hai phương OA và OB (hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần?
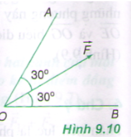
A. F1 = F2 = F
B. F1 = F2 = F/2
C. F1 = F2 = 1,15F
D. F1 = F2 = 0,58F
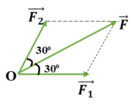
Áp dụng quy tắc hình bình hành: Từ điểm ngọn của vecto F lần lượt vẽ các đoạn song song với hai phương OA và OB ta được các vecto F1 trên OA và F2 trên OB sao cho
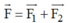
Hình bình hành có đường chéo cũng là đường phân giác của 1 góc nên nó là hình thoi.
Suy ra: F1 = F2
Mà
Đúng 0
Bình luận (0)
Một vật chịu tác dụng của 2 lực song song cùng chiều có độ lớn lần lượt là
F
1
20
N
,
F
2
, hợp lực của chúng có độ lớn F 50N và giá của hợp lực
F
→
cách giá của
F
1
→
một đoạn 30cm. Độ lớn của
F...
Đọc tiếp
Một vật chịu tác dụng của 2 lực song song cùng chiều có độ lớn lần lượt là F 1 = 20 N , F 2 , hợp lực của chúng có độ lớn F = 50N và giá của hợp lực F → cách giá của F 1 → một đoạn 30cm. Độ lớn của F 2 → lực F 2 → và khoảng cách từ giá hợp lực đến giá là:
A. 30 N và 20 cm
B. 20 N và 20 cm
C. 70 N và 30 cm
D. 30 N và 30 cm
