Cho F(x) là một nguyên hàm của hàm số f ( x ) = x 4 - 2 x 3 + 1 x 2 và F(3)=-1. Tìm F(-1)
A. -2
B. - 5 3
C. - 7 3
D. -1
Cho hàm số F ( x ) = a x 3 + b x 2 + c x + 1 là một nguyên hàm của hàm số f(x) thỏa mãn f(1) = 2, f(2) = 3, f(3) = 4. Hàm số F(x) là
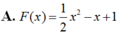
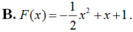
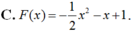
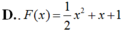
Chọn D.
Ta có
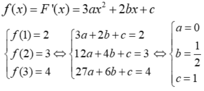
Vậy F(x)= 1 2 x 2 + x + 1
Cho F ( x ) = - 1 3 x 3 là một nguyên hàm của hàm số f ( x ) x Tìm nguyên hàm của hàm số f'(x)lnx
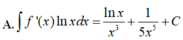
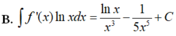
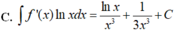
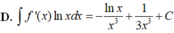
Cho F ( x ) = ( x - 1 ) e x là một nguyên hàm của hàm số f ( x ) e 2 x . Tìm nguyên hàm của hàm số f ' ( x ) e 2 x
![]()
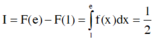
![]()
![]()
Cho F ( x ) = x 2 là một nguyên hàm của hàm số f ( x ) e 2 x . Tìm nguyên hàm của hàm số f ' ( x ) e 2 x
![]()
![]()
![]()
![]()
Cho F ( x ) = 1 4 x 4 + 1 3 x 3 là một nguyên hàm của hàm số f(x). Tìm nguyên hàm của hàm số f’(x)cosx
A. ∫ f ' x cos x d x = 2 x + 1 sin x - 2 cos x + C
B. ∫ f ' x cos x d x = 2 x + 1 sin x + 2 cos x + C
C. ∫ f ' x cos x d x = - 2 x + 1 sin x - 2 cos x + C
D. ∫ f ' x cos x d x = - 2 x + 1 sin x + 2 cos x + C
Cho hàm số f(x)=1/x. Nếu F(x) là một nguyên hàm của hàm số f(x) và đồ thị hàm số y=F(x) đi qua M(-1;0) thì F(x) là
![]()
![]()
![]()
![]()
Cho hàm số f ( x ) = x 2 ( x - 1 ) e 3 x có một nguyên hàm là hàm số f(x). Số điểm cực trị của hàm số f(x) là
A. 1
B. 2
C. 3
D. 0
Cho hàm số F(x) là một nguyên hàm của hàm số f ( x ) = sin 3 x cos x . Tính I = F ( π 2 ) - F ( 0 )
A. I = π 2
B. I = 1 4
C. I = 3 π 2
D. I = 3 4
Cho hàm số f(x) liên tục trên ℝ và có một nguyên hàm là F(x). Biết F(2) = –7. Giá trị của F(4) là:
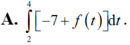
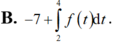
![]()
![]()
Chọn B
Theo định nghĩa tích phân ta có
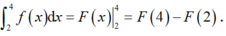
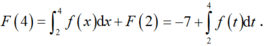
Cho F(x) là một nguyên hàm của hàm số f(x) = xln x . Tính F''(x).
![]()
![]()
![]()
![]()