Chứng minh phân thức 12 n + 1 30 n + 2 là tối giản với mọi số tự nhiên n
PB
Những câu hỏi liên quan
chứng minh phân số 12.n+1 phần 30.n+2 là phân số tối giản
Chứng minh rằng: 12*n/30*2 là phân số tối giản
chứng tỏ phân số 12.n + 1 / 30.n + 2 là phân số tối giản ( n thuộc N )
Gọi ƯCLN(12n + 1,30n + 2) là d
Ta có: 12n + 1 chia hết cho d => 5(12n + 1) chia hết cho d => 60n + 5 chia hết cho d
30n + 2 chia hết cho d => 2(30n + 2) chia hết cho d => 60n + 4 chia hết cho d
=> 60n + 5 - (60n + 4) chia hết cho d
=> 60n + 5 - 60n - 4 chia hết cho d
=> 1 chia hết cho d => d = 1
=> ƯCLN(12n + 1,30n + 2) = 1
Vậy \(\frac{12n+1}{30n+2}\)là phân số tối giản
Đúng 0
Bình luận (0)
Cho phân thức m n là phân thức tối giản. Chứng minh phân thức m m + n là phân thức tối giản
Hướng dẫn giải:
Giả sử m, n là các số nguyên và ƯCLN(m, n) = 1 (vì 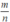 tối giản)
tối giản)
nếu d là ước chung m của m + n thì:
(m + n) d và m d
⇒ [(m + n) – m ] = n d
⇒ d ∈ ƯC (m,n) ⇒ d = 1(vì 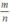 tối giản) .
tối giản) .
Vậy nếu phân thức 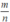 là phân thức tối giản thì phân thức
là phân thức tối giản thì phân thức 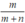 cũng là phân thức tối giản.
cũng là phân thức tối giản.
Đúng 0
Bình luận (0)
A=n+1/n+2 là phân số tối giản vớ mọi số nguyên n khác -2
Chứng minh phân thức 3 n + 1 5 n + 2 (với n ∈ N) là tối giản
Hướng dẫn giải:
Gọi ƯCLN của 2n + 1 và 5n + 3 là d
⇒ (3n + 1) ⋮ d và (5n + 2) ⋮ d
⇒ [3(5n + 2) - 5(3n + 1)] ⋮ d
⇒ 1 ⋮ d, với ∀n ∈ N
⇒ d = 1 hoặc d = -1
Vậy phân thức đã cho tối giản với ∀n ∈ N
Đúng 1
Bình luận (0)
1)chứng tỏ phân số sau là phân số tối giản
\(12.n+1/30.n+2 \)
2)chứng tỏ phn số sau là phân số tối giản
\(3.n+2/3.n+2\)
Chứng minh rằng n7+n2+1/n8+n+1 chưa phải là phân thức tối giản
chứng minh các phân số sau là các phân số tối giản
a,A= 12n+1/30n+2 b,B= 14n+17/21n+25
a)
Gọi d là Ư CLN (12n+1 ; 30n+2)
⇒12n+1 ⋮ d và 30n+2 ⋮d
⇒(5*12)n+5 ⋮d và (2*30)n+4 ⋮d
⇔60n+5 ⋮d và 60n+4 ⋮d
Suy ra: (60n+5 - 60n+4) ⋮d
1 ⋮d
⇒d=1 ⇒ƯCLN(12n+1;30n+2)=d=1 ⇒đpcm
b)
Gọi ƯCLN(14n+17;21n+25) là d
⇒14n+17⋮d và 21n+25⋮d
⇒ 3·14n+3·17⋮d và 2·21n+2·25⋮d
⇔42n+51⋮d và 42n+50⋮d
⇔(42n+51 - 42n+50) ⋮d
⇒1 ⋮d
⇒d=1
Vậy ƯCLN(14n+17;21n+25)=d=1
⇒đpcm
Đúng 0
Bình luận (0)
a Ta có : A là p/số tối giản <=> ƯCLN(12n + 1; 30n + 2) \(\in\){1; -1}
Gọi d là ƯCLN(12n + 1; 30n + 2)
=> 12n + 1 \(⋮\)d => 5(12n + 1) \(⋮\)d => \(60n+5⋮d\)
30n + 2 \(⋮\)d => 2(30n + 2) \(⋮\)d => \(60n+4⋮d\)
=> (60n + 5) - (60n + 4) = 1 \(⋮\)d \(\in\){1; -1}
Vậy A là p/số tối giản
Đúng 0
Bình luận (0)
Chứng minh phân số sau đây tối giản vớ mọi \(n\in Z\)
\(\frac{n+3}{n+2}\)
gọi d là UCLN(n+3;n+2)
ta có:
n+3-n+2 chia hết d
=>1 chia hết d
=>d=±1
=>ps tối giản
Đúng 0
Bình luận (0)
Tôi giải thế này có đúng ko???
Gọi d = ƯC ( n + 3; n + 2 )
Ta có: ( n + 3 ) chia hết cho d => ( n + 3 ) - ( n + 2 ) chia hết cho d => 1 chia hết cho d.
=> d = +_ 1
=> Tử và mẫu có ƯC = 1 và -1
=> Phân số trên tối giản
Đúng 0
Bình luận (0)
Gọi UCLN(n+3,n+2)=d
Ta có:n+3 chia hết cho d
n+2 chia hết cho d
=>(n+3)-(n+2) chia hết cho d
=>1 chia hết cho d
=>d=1
Vậy phân số trên tối giản với mọi n\(\in\)Z
Đúng 0
Bình luận (0)
Xem thêm câu trả lời


