Xét sự biến thiên của hàm số y = x x − 1 . Chọn khẳng định đúng.
A. Hàm số nghịch biến trên từng khoảng xác định của nó
B. Hàm số đồng biến trên từng khoảng xác định của nó.
C. Hàm số đồng biến trên (− ∞ ; 1), nghịch biến trên (1; + ∞ ).
D. Hàm số nghịch biến trên ( − ∞ ; 1 ) ∪ ( 1 ; + ∞ ) .




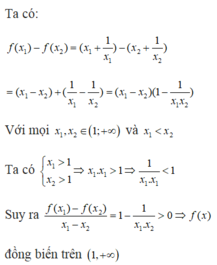
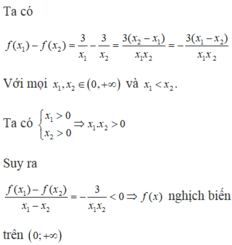

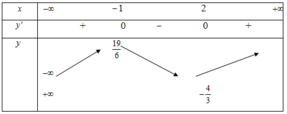
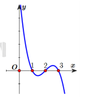 Xét các khẳng định sau:
Xét các khẳng định sau: