Cho hàm số y= x4- 2mx2+m (1) với m là tham số thực. Gọi (C) là đồ thị hàm số (1); d là tiếp tuyến của (C) tại điểm có hoành độ bằng 1. Tìm m để khoảng cách từ điểm B( ¾; 1) đến đường thẳng d đạt giá trị lớn nhất?
A. 0
B. 1
C. 2
D. 3
Cho hàm số y = x 4 − 2 m x 2 + m C với m là tham số thực. Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1. Tìm tham số m để tiếp tuyến ∆ với đồ thị (C) tại A cắt đường tròn T : x 2 + y − 1 2 = 4 tạo thành một dây cung có độ dài nhỏ nhất
A. m = 16 13
B. m = - 13 16
C. m = 13 16
D. m = − 16 13
Đáp án C
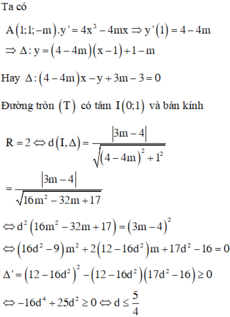
Để dây cung có độ dài nhỏ nhất = 5 4 ⇒ m = 13 16
Cho hàm số y=x4-2mx2+2 với m là tham số thực. Có bao nhiêu giá trị nguyên của m để đồ thị hàm số có ba điểm cực trị A; B; C thỏa mãn OA.OB.OC=12?
A.2
B.1
C.0
D.4
Để hàm số có ba điểm cực trị khi và chỉ khi ab< 0 hay 1.( -2m) <0
Suy ra m> 0
Khi đó
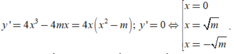
Suy ra tọa độ các điểm cực trị của đồ thị hàm số là:
A 0 ; 2 , B m ; - m 2 + 2 , C - m ; - m 2 + 2
Ycbt O A . O B . O C = 12 ⇔ 2 m + - m 2 + 2 2 = 12
Giải ra ta được m=2; có một giá trị nguyên.
Chọn B.
Cho hàm số
y = - x 4 + 2 m x 2 - 2 m + 1 (m tham số)
có đồ thị là (Cm).
Biện luận theo m số cực trị của hàm số.
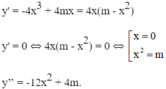
- Nếu m ≤ 0, phương trình y’ = 0 có nghiệm duy nhất x = 0.
Mà y’’(0) = 4m < 0
⇒ x = 0 là điểm cực đại và là cực trị duy nhất của hàm số.
- Nếu m > 0 thì phương trình (1) có 2 nghiệm phân biệt khác 0 nên phương trình y’= 0 có 3 nghiệm
⇒ hàm số có 3 cực trị.
Với m là một tham số thực sao cho đồ thị hàm số y = x 4 + 2 m x 2 + 1 có ba điểm cực trị tạo thành một tam giác vuông. Mệnh đề nào dưới đây đúng ?
A. m < -2
B. - 2 ≤ m < 0
C. 0 ≤ m < 2
D. 2 ≤ m
Cho hàm số
y = - x 4 + 2 m x 2 - 2 m + 1 (m tham số)
có đồ thị là C m .
Với giá trị nào của m thì C m cắt trục hoành?
– Xét m ≤ 0, phương trình y’ = 0 có nghiệm duy nhất x = 0.
Ta có bảng biến thiên :
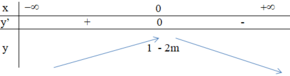

Ta có bảng biến thiên :
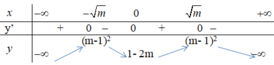

Cho hàm số
y = - x 4 + 2 m x 2 - 2 m + 1 (m tham số)
có đồ thị là C m .
Xác định để C m có cực đại, cực tiểu.
Dựa vào bảng biến thiên phần b) ta có :
C m có cực đại, cực tiểu ⇔ m > 0
Gọi m 0 là giá trị thực của tham số m để đồ thị hàm số y = x 4 + 2 m x 2 + 4 có 3 điểm cực trị nằm trên các trục tọa độ. Khẳng định nào sau đây là đúng?
A. m 0 ∈ 1 ; 3
B. m 0 ∈ − 5 ; − 3
C. m 0 ∈ − 3 2 ; 0
D. m 0 ∈ − 3 ; − 3 2
Đáp án D
y ' = 4 x 3 + 4 m x y ' = 0 ⇔ x = 0 x 2 = − m
Hàm số có 3 cực trị ⇔ m < 0 Khi đó đồ thị hàm số có 3 cực trị là A 0 ; 4 , B − − m ; − m 2 + 4 , C − m ; − m 2 + 4
Ta có A ∈ O y nên 3 điểm cực trị nằm trên các trục tọa độ ⇔ − m 2 + 4 = 0 ⇔ m = 2 K T M m = − 2 T M
Cho hàm số y = x 4 - 2 m x 2 + 3 m - 2 (với m là tham số). Có bao nhiêu giá trị của tham số m để các điểm cực trị của đồ thị hàm số đều nằm trên các trục tọa độ?
A. 2
B. 0
C. 3
D. 1
Cho hàm số y = x 4 - 2 m x 2 + m - 1 . Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số có ba điểm cực trị tạo thành 1 tam giác nhận gốc tọa độ O làm trực tâm .
A. m = 4
B. m = 2
C. m = 3
D. m = 1
Chọn D
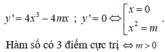
Khi đó đồ thị hàm số có 3 điểm cực trị là:
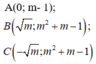
Vì B, C đối xứng với nhau qua trục tung nên B C ⊥ O A
Do đó O là trực tâm tam giác:
![]()
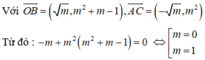
Kết hợp điều kiện, vậy m = 1 là giá trị cần tìm