Kí hiệu F(x) là một nguyên hàm của hàm số f x = 1 e x + 1 , biết F 0 = − ln 2 . Tìm tập nghiệm S của phương trình F x + ln e x + 1 = 3 .
A. S = − 3 ; 3
B. S = 3
C. S = ∅
D. S = − 3
Kí hiệu F(x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F(0) = -ln2. Tìm tập nghiệm S của phương trình
A. S = {-3;3}
B. S = {3}
C. S = ∅
D. S = {-3}
Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .
A. S = - 3 ; 3
B. S = 3
C. S = ∅
D. S = - 3
Đáp án B
∫ 1 e x + 1 d x = ∫ d x - ∫ e x e x + 1 d x = x - ln ( e x + 1 ) + C
Vì F ( 0 ) = = - ln 2 ⇔ C = 0 ⇒ F ( x ) = x - ln e x + 1
Xét phương trình F ( x ) + ln ( e x + 1 ) = 3 ⇔ x = 3
Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(1)-F(2) bằng
A. ∫ 1 2 f x d x
B. ∫ 1 2 - f x d x
C. ∫ 2 1 - F x d x
D. ∫ 1 2 - F x d x
Cho F(x) là một nguyên hàm của hàm số f(x). Khi đó hiệu số F(0) – F(1) bằng
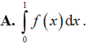
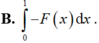

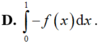
Một nguyên hàm F(x) của hàm số f ( x ) = e - x + e x 2 thỏa mãn F(0) = 1 là
![]()
![]()
![]()
![]()
Cho hàm số f(x) là một nguyên hàm của hàm số y = e x x ≥ 1 e - x x ≤ 1 với f(1)=e. Giá trị biểu thức f(-ln3)+f(-ln2)+f(ln2)+f(ln3) bằng
A. 2 e + 1 e
B. 3 e + 1 e - 10 3
C. 3 e + 1 e - 5 2
D. 3 e + 1 e + 21 2
Biết hàm số F(x) là một nguyên hàm của hàm số f ( x ) = ln x x ln 2 x + 3 có đồ thị đi qua điểm (e; 2016) . Khi đó hàm số F(1) là
A. 3 + 2014
B. 3 + 2016
C. 2 3 + 2014
D. 2 3 + 2016
Chọn A.
Đặt t = ln 2 x + 3 và tính được F(x)= ln 2 x + 3 + C
F(e)=2016=>C=2014=>F(x)= ln 2 x + 3 + 2014 ⇒ F ( 1 ) = 3 + 2014
Cho hai hàm số F(x)= ( x 2 + a x + b ) e - x v à f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a=1;b= -7
B. a= -1;b= -7
C. a= -1;b=7
D. a=1;b=7
Cho hai hàm số F ( x ) = ( x 2 + a x + b ) e - x và f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a = 1 b = -7
B. a = -1 b = -7
C. a = -1 b = 7
D. a = 1 b = 7