giá trị nguyên nhỏ nhất của x thoả mãn /2-x/=x-2
H24
Những câu hỏi liên quan
Cho
z
x
+
y
i
với x, y
∈
R
là số phức thỏa mãn điều kiện
z
¯
+
2
-
3
i
≤
|
z
+
i
-
2
|
≤
5
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ...
Đọc tiếp
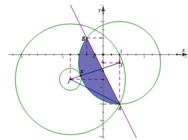
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
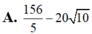
![]()
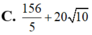
![]()
Cho các số nguyên x,y thỏa mãn 5x - 2y =1. Tìm giá trị nhỏ nhất của biểu thức \(T=3|x|+5|y|\)
Cho các số nguyên x,y thỏa mãn 5x-2y=1. Tìm giá trị nhỏ nhất của biểu thức \(T=3|x|+5|y|\)
bạn ơi. Bạn có đáp án của bài này chưa vậy. Cho mik xin vs
mik đang cần gấp
Đúng 0
Bình luận (0)
Bài 1 :
a) Tìm giá trị nhỏ nhất của A = l x - 2 l + 5
b) Tìm giá trị nhỏ nhất của B = 12 - l x + 4 l
c) Tìm giá trị nhỏ nhất của C = (căn bậc hai x) + 1
tập hợp các giá trị của x thoả mãn {x-1}X{x+2}=0
=> x - 1 = 0 => x = 1
hoặc x + 2 = 0 => x = -2
Vậy: x thuộc {-2;1}
Đúng 0
Bình luận (0)
a) Tìm các giá trị nguyên của x để phân số sau nhận các giá trị nguyên:
A= 6x +9/ 3x+2
b) Tìm giá trị nhỏ nhất của biểu thức :
A=| x | + | 8-x |
\(a)\) Ta có :
\(A=\frac{6x+9}{3x+2}=\frac{6x+4+5}{3x+2}=\frac{6x+4}{3x+2}+\frac{5}{3x+2}=\frac{2\left(3x+2\right)}{3x+2}+\frac{5}{3x+2}=2+\frac{5}{3x+2}\)
Để A có giá trị nguyên thì \(\frac{5}{3x+2}\) phải nguyên hay \(5\) chia hết cho \(3x+2\)\(\Rightarrow\)\(\left(3x+2\right)\inƯ\left(5\right)\)
Mà \(Ư\left(5\right)=\left\{1;-1;5;-5\right\}\)
Suy ra :
| \(3x+2\) | \(1\) | \(-1\) | \(5\) | \(-5\) |
| \(x\) | \(\frac{-1}{3}\) | \(-1\) | \(1\) | \(\frac{-7}{3}\) |
Mà \(x\) là số nguyên nên \(x\in\left\{-1;1\right\}\)
Vậy \(x\in\left\{-1;1\right\}\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
\(b)\) Ta có bất đẳng thức giá trị tuyệt đối như sau :
\(\left|x\right|+\left|y\right|\ge\left|x+y\right|\)
Dấu "=" xảy ra khi và chỉ khi \(xy\ge0\)
Áp dụng vào ta có :
\(A=\left|x\right|+\left|8-x\right|\ge\left|x+8-x\right|=\left|8\right|=8\)
Dấu "=" xảy ra khi và chỉ khi \(x\left(8-x\right)\ge0\)
Trường hợp 1 :
\(\hept{\begin{cases}x\ge0\\8-x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge0\\x\le8\end{cases}\Leftrightarrow}0\le x\le8}\)
Trường hợp 2 :
\(\hept{\begin{cases}x\le0\\8-x\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le0\\x\ge8\end{cases}}}\) ( loại )
Vậy GTNN của \(A=8\) khi \(0\le x\le8\)
Chúc bạn học tốt ~
Đúng 0
Bình luận (0)
[...]5chia hết 3x+2
3x+2thuoc tập ước của 5
[...]
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho các số thực a,b,c thoả mãn (a^2)+(b^2)+(c^2)=2 . Tìm giá trị lớn nhất nhỏ nhất cuả biểu thức M=a+b+c-abc
Với giá trị nào của x và y thì biểu thức A có giá trị nhỏ nhất?Giá trị nhỏ nhất đó bằng bao nhiêu? A= |x - 10| + |y + 100| - 2
Ta thấy: |x-10| >= 0 (1); |x-10| >= 0 (2)
Cộng 2 bđt cùng chiều (1) và (2) ta được: |x-10| + |x-10| >= 0 <=> A= |x-10| + |x-10| -2 >= -2
=> minA = -2
Dấu đẳng thức xảy ra khi và chỉ khi x=10 và y=-100
Chắc v!! =)))
Đúng 0
Bình luận (0)
Cho 2 số x,y thỏa mãn \(5x^2+8xy+5y^2=36\). Tìm giá trị nhỏ nhất của M=\(x^2+y^2\)
Đề là tìm GTLN chứ nhỉ ?
Ta có : \(5x^2+8xy+5y^2=36\)
\(\Leftrightarrow x^2+y^2+4\left(x^2+2xy+y^2\right)=36\)
\(\Leftrightarrow M+4\left(x+y\right)^2=36\)
\(\Leftrightarrow M=36-4\left(x+y\right)^2\le36\)
Dấu ''=" khi x = -y
Thế vào pt ban đầu sẽ tìm đc giá trị cụ thể của x ; y
Đúng 0
Bình luận (0)