Cho hai hàm số F x = x 2 + a x + b e - x và f x = - x 2 + 3 x + 6 e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a = 1, b = -7
B. a = -1, b = -7
C. a = -1, b = =7
D. a = 1, b = 7
Cho hai hàm số \(f\left( x \right) = {x^3} + x\) và \(g\left( x \right) = {x^2} + 1\,\,\left( {x \in \mathbb{R}} \right).\) Hãy cho biết:
a) Hai hàm số \(f\left( x \right),g\left( x \right)\) có liên tục tại \(x = 2\) hay không.
b) Các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) có liên tục tại \(x = 2\) hay không.
a) Ta có \(f\left( x \right),g\left( x \right)\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right),g\left( x \right)\) liên tục tại \(x = 2\)
b) \(\begin{array}{l}f\left( x \right) + g\left( x \right) = {x^3} + {x^2} + x + 1\\f\left( x \right) - g\left( x \right) = {x^3} - {x^2} + x - 1\\f\left( x \right).g\left( x \right) = \left( {{x^3} + x} \right)\left( {{x^2} + 1} \right) = {x^5} + 2{x^3} + x\\\frac{{f\left( x \right)}}{{g\left( x \right)}} = \frac{{{x^3} + x}}{{{x^2} + 1}} = \frac{{x\left( {{x^2} + 1} \right)}}{{{x^2} + 1}} = x\end{array}\)
Ta có \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) là các hàm đa thức nên các hàm số \(f\left( x \right),g\left( x \right)\) liên tục trên \(\mathbb{R}\)
Vậy các hàm số \(f\left( x \right) + g\left( x \right);f\left( x \right) - g\left( x \right);f\left( x \right).g\left( x \right);\frac{{f\left( x \right)}}{{g\left( x \right)}}\) liên tục tại \(x = 2\)
Cho hai hàm số F(x)= ( x 2 + a x + b ) e - x v à f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a=1;b= -7
B. a= -1;b= -7
C. a= -1;b=7
D. a=1;b=7
Cho hai hàm số F ( x ) = ( x 2 + a x + b ) e - x và f ( x ) = ( - x 2 + 3 x + 6 ) e - x . Tìm a và b để F(x) là một nguyên hàm của hàm số f(x)
A. a = 1 b = -7
B. a = -1 b = -7
C. a = -1 b = 7
D. a = 1 b = 7
a) Cho hàm số y=f(x)=-2x+3.Tính f(-2);f(-1);f(0);f(-1/2);f(1/2)
b) Cho hàm số y=g(x)=x^2-1.Tính g(-1);g(0);g(1);g(2)
c)Với giá trị nào của x để hai hàm số trên nhận cùng giá trị
Làm bài c thôi ạ mấy câu còn lại nháp thôi ạ.
Cho hàm số bậc hai \(y = f(x) = {x^2} - 4x + 3\)
a) Xác định hệ số a. Tính \(f(0);f(1);f(2);f(3);f(4)\) và nhận xét về dấu của chúng so với dấu của hệ số a
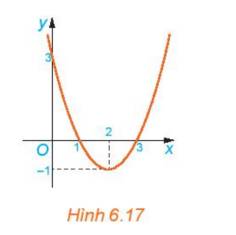
b) Cho đồ thị hàm số y=f(x) (H.6.17). Xét từng khoảng \(\left( { - \infty ;1} \right);\left( {1;3} \right);\left( {3; + \infty } \right)\), đồ thị nằm phía trên hay phía dưới trục Ox?
c) Nhận xét về dấu của f(x) và dấu của hệ số a trên từng khoảng đó.
a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a
cho hai hàm số : f(x) = x^2 và g(x) = 3 - x .
a) Tính f(-3) , f(-1/2) , f(0) , g(1) , g(2) , g(3) .
b) Xác định a để 2f(a) = g(a) .
\(a,f\left(-3\right)=9;f\left(-\dfrac{1}{2}\right)=\dfrac{1}{4};f\left(0\right)=0\\ g\left(1\right)=2;g\left(2\right)=1;g\left(3\right)=0\\ b,2f\left(a\right)=g\left(a\right)\\ \Leftrightarrow2a^2=3-a\\ \Leftrightarrow2a^2+a-3=0\\ \Leftrightarrow2a^2-2a+3a-3=0\\ \Leftrightarrow2a\left(a-1\right)+3\left(a-1\right)=0\\ \Leftrightarrow\left(2a+3\right)\left(a-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=1\\a=-\dfrac{3}{2}\end{matrix}\right.\)
a) cho hàm số y=(f)x=x^6+1/x^3.cmr f(1/2)=f(x)
b) cho hàm số y=(f)x=x^2+1/x^2.CMR f(x)=f(-x)
c) cho hàm số y=(f)x=5^x. Tính f(x+1)-f(x)
HELPPPPPPPPPPPPP ME!
a) Cho hàm số
y = f ( x ) = 2 3 x
Tính: f(-2); f(-1); f(0); f(1/2); f(1); f(2); f(3)
b) Cho hàm số
y = g ( x ) = 2 3 x + 3
Tính: g(-2); g(-1); g(0); g(1/2); g(1); g(2); g(3)
c) Có nhận xét gì về giá trị của hai hàm số đã cho ở trên khi biến x lấy cùng một giá trị?
a) Ta có:
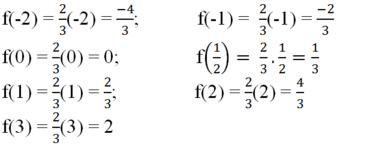
b) Ta có:
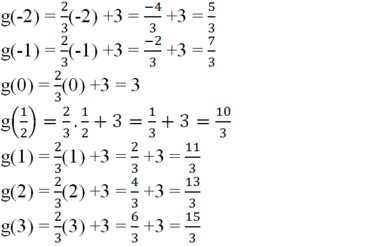
c) Từ kết quả câu a, b ta được bảng sau:

Nhận xét:
- Hai hàm số
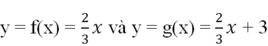
là hai hàm số đồng biến vì khi x tăng thì y cũng nhận được các giá trị tương ứng tăng lên.
- Cùng một giá trị của biến x, giá trị của hàm số y = g(x) luôn luôn lớn hơn giá trị tương ứng của hàm số y = f(x) là 3 đơn vị.
Cho hàm số y = f ( x ) liên tục trên R \ { - 1 ; 0 } thỏa mãn f ( 1 ) = 2 ln 2 + 1 , x ( x + 1 ) f ' ( x ) + ( x + 2 ) f ( x ) = x ( x + 1 ) , ∀ x ∈ R \ { - 1 ; 0 } Biết f ( 2 ) = a + b ln 3 với a, b là hai số hữu tỉ. Tính T = a 2 - b
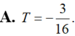
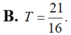
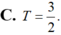
![]()
Cho hàm số y = f ( x ) liên tục trên ℝ \ − 1 ; 0 thỏa mãn f ( 1 ) = 2 ln 2 + 1 , x ( x + 1 ) f ' ( x ) + ( x + 2 ) f ( x ) = x ( x + 1 ) , ∀ x ∈ ℝ \ − 1 ; 0 . Biết f ( 2 ) = a + b ln 3 , với a, b là hai số hữu tỉ. Tính T = a 2 − b
A. T = − 3 16 .
B. T = 21 16 .
C. T = 3 2 .
D. T = 0