Trong không gian với hệ tọa độ Oxyz cho ba điểm A 1 , 0 , 0 , B 0 , 2 , 0 , C 0 , 0 , 3 . Tập hợp các điểm M x , y , z thỏa M A 2 = M B 2 + M C 2 là mặt cầu có bán kính
A. R = 2
B. R = 3
C. R = 2
D. R = 3
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; 0; 2), B(3; 0; 5), C(1; 1; 0). Tọa độ của điểm D sao cho ABCD là hình bình hành là
A. D(4; 1; 3)
B. D(-4; -1; -3)
C. D(2; 1; -3)
D. D(-2; 1; -3)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1; 0; 0), B(0; -2; 0), C(0; 0; -5). Vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng (ABC)
A. n → = ( 1 ; 1 2 ; 1 5 )
B. n → = ( 1 ; - 1 2 ; - 1 5 )
C. n → = ( 1 ; - 1 2 ; 1 5 )
D. n → = ( 1 ; 1 2 ; - 1 5 )
Trong không gian Oxyz với hệ tọa độ Oxyz, cho ba điểm A(2;-1;1), B(1;0;4) và C(0;-2;-1). Phương trình mặt phẳng qua A và vuông góc với đường thẳng BC là
A. 2 x + y + 2 z - 5 = 0
B. x + 2 y + 5 z + 5 = 0
C. x - 2 y + 3 z - 7 = 0
D. x + 2 y + 5 z - 5 = 0
Trong không gian với hệ tọa độ Oxyz, cho A(1 ;-2 ;0), B(0 ;2 ;0), C(2 ;1 ;3). Tọa độ điểm M thỏa mãn M A → - M B → + M C → = 0 → là:
A. (3;2;-3)
B. (3;-2;3)
C. (3;-2;-3)
D. (3;2;3)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A ( 3 ; 0 ; 0 ) , B ( 0 ; – 4 ; 0 ) , C ( 0 ; 0 ; 4 ) . Viết phương trình mặt phẳng (R) đi qua ba điểm A, B, C.
A. ( R ) : 4 x – 3 y + 3 z – 12 = 0
B. ( R ) : 4 x + 3 y + 3 z + 12 = 0
C. ( R ) : 3 x – 4 y + 4 z – 12 = 0
D. ( R ) : 3 x + 4 y + 4 z + 12 = 0 .
Đáp án là A
(R) là mặt phẳng có phương trình đoạn chắn là
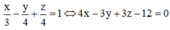
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(3;0;0), B(0;–4;0), C(0;0;4). Viết phương trình mặt phẳng (R) đi qua ba điểm A, B, C
A. (R) : 4x – 3y + 3z – 12 = 0
B. (R) : 4x + 3y + 3z + 12 = 0
B. (R) : 3x – 4y + 4z – 12 = 0
D. (R) : 3x + 4y + 4z + 12 = 0
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(0;-2;-1), B(-2;-4;3), C(1;3;-1). Tìm điểm MÎOxy sao cho M A → + M B → + 3 M C → đạt giá trị nhỏ nhất
A. 1 5 ; 3 5 ; 0
B. - 1 5 ; 3 5 ; 0
C. 1 5 ; - 3 5 ; 0
D. 3 4 ; 4 5 ; 0
Trong không gian với hệ tọa độ Oxyz, cho ba vectơ a → = 2 ; 3 ; − 5 ; b → = 0 ; − 3 ; 4 ; c → = 1 ; − 2 ; 3 . Tọa độ vectơ n → = 3 a → + 2 b → − c → là:
A. n → = 5 ; 1 ; − 10
B. n → = 7 ; 1 ; − 4
C. n → = 5 ; 5 ; − 10
D. n → = 5 ; − 5 ; − 10
Đáp án C
n → = 3 2 ; 3 ; − 5 + 2 0 ; − 3 ; 4 − 1 ; − 2 ; 3 = 5 ; 5 ; − 10
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ A B → là
A. A B → = 1 ; - 1 ; 1
B. A B → = 1 ; 1 ; - 3
C. A B → = 3 ; - 3 ; 3
D. A B → = 3 ; - 3 ; - 3
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(0;1;2), B(2;-2;1), C(-2;0;1) và mặt phẳng ( P ) : 2 x + 2 y + z - 3 = 0 . Tọa độ điểm M thuộc mặt phẳng (P) sao cho M cách đều ba điểm A, B, C là
A. M(-7;3;2)
B. M(2;3;-7)
C. M(3;2;-7)
D. M(3;-7;2)
Chọn B
Đặt M(x;y;z). Lập hệ 3 phương trình ba ẩn x,y,z từ phương trình mặt phẳng (P) và điều kiện MA=MB, MA=MC