Cho mặt phẳng ( α ) đi qua điểm M(1; –3;4) và song song với mặt phẳng ( β ) : 6x + 2y – z – 7 = 0. Phương trình mặt phẳng ( α ) là :
A. 6x + 2y – z +8 = 0
B. 6x + 2y – z +4 = 0
C. 6x + 2y – z – 4 = 0
D. 6x + 2y – z – 17 = 0
Cho điểm M(3;-1;-2) và mặt phẳng α : 3x-y+z+4=0. Phương trình nào sau đây là phương trình mặt phẳng đi qua M và song song với α
![]()
![]()
![]()
![]()
Cho điểm M 3 ; - 1 ; - 2 và mặt phẳng α : 3 x - y + z + 4 = 0 . Phương trình nào sau đây là phương trình mặt phẳng đi qua M và song song với (α)?
A. 3x-y+2z-6=0
B. 3x-y+2z+6=0
C. 3x+y-2z-14=0
D. 3x-y-2z+6=0
Trong không gian với hệ tọa độ Oxyz, cho (α) là mặt phẳng đi qua điểm M(1; - 2; 4) và có véc-tơ pháp tuyến ![]() =(2; 3; 5). Phương trình mặt phẳng (α) là:
=(2; 3; 5). Phương trình mặt phẳng (α) là:
A. 2x + 3y + 5z - 16=0
B. x - 2y + 4z - 16=0
C. 2x + 3y + 5z + 16=0
D. x - 2y + 4z=0.
Đáp án A
Phương trình mặt phẳng (α): 2(x - 1) + 3(y + 2) + 5(z - 4)=0<=> 2x + 3y + 5z - 16=0.
Trong không gian với hệ tọa độ Oxyz cho điểm M (3;-1;-2) và mặt phẳng ( α ): 3x-y+2z+4=0. Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với ( α )?
A. 3x+y-2z-14=0
B. 3x-y+2z+6=0
C. 3x-y+2z-6=0
D. 3x-y-2z+6=0
Đáp án C
Phương trình mặt phẳng qua M và song song với ( α ) là:
3(x-3)-(y+1)+2(z+2)=0 ⇔ 3x-y+2z-6=0
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0 Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).
M’ đối xứng với M qua (α)
⇒ H là trung điểm MM’
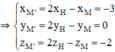
⇒ M’(-3; 0; -2).
Cho điểm M(1; -1; 2) và mặt phẳng ( α ): 2x – y + 2z + 12 = 0. Tìm tọa độ điểm M’ đối xứng với M qua mặt phẳng ( α )
H là trung điểm của MM’, suy ra x M ' = 2 x H - x M = −67/9
y M ' = 2 y H - y M = 29/9
z M ' = 2 z H - z M = −58/9
Vậy ta được ![]()
Trong không gian với hệ tọa độ Oxyz cho điểm M 1 ; 0 ; 6 và mặt phẳng α có phương trình là x + 2 y + 2 z − 1 = 0 . Viết phương trình mặt phẳng β đi qua M và song song với α
A. β : x + 2 y + 2 z + 13 = 0.
B. β : x + 2 y + 2 z − 15 = 0.
C. β : x + 2 y + 2 z − 13 = 0.
D. β : x + 2 y + 2 z + 15 = 0.
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng α : 2 x - y - 3 z + 10 = 0 và điểm M(2;-2;3). Mặt phẳng (P) đi qua M và song song với mặt phẳng α có phương trình là:
![]()
![]()
![]()
![]()
Cho mặt phẳng ( α ) đi qua M(1; - 3;4) và song song với mặt phẳng ( β ) : 6x – 5y +z – 7 = 0. Phương trình mặt phẳng ( α ) là:
A. 6x - 5y + z + 25 = 0
B. 6x - 5y + z - 25 = 0
C. 6x - 5y + z - 7 = 0
D. 6x - 5y + z + 17 = 0
Đáp án B.
Phương pháp: Mặt phẳng ( α ) đi qua M(1; - 3;4) và nhận n β → = 6 ; - 5 ; 1 là 1 VTPT.
Cách giải: Mặt phẳng ( α ) đi qua M(1; - 3;4) và nhận n β → = 6 ; - 5 ; 1 là 1 VTPT nên có phương trình:
6(x - 1) - 5(y+3)+(z - 4)=0
→ 6x - 5y + z - 25 = 0