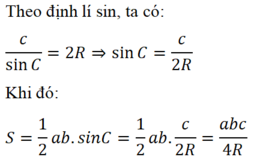Chứng minh công thức S = pr
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
Chứng minh rằng diện tích ∆ ngoại tiếp một dường tròn được timhs theo công thức: S=pr, trong đó p là nửa chu vi ∆,r là bán kính đường tròn nội tiếp.
chứng minh công thức S=\(\frac{S.100\%}{100+S}\)
Dựa vào công thức (1) và định lý sin, hãy chứng minh S = abc/4R.
PA
30 tháng 6 2023 lúc 13:05
Với `p;q;r;s\inRR : {(p+q+r+s=0),(p<q<r<s):}` chứng minh rằng: `p<1/2 \root[3]{(\sqrt(24(pq+pr+ps+qr+qs+rs)^3+81(pqr+qrs+rsp+spq)^2)+9(pqr+qrs+rsp+spq))/(9)}-(pq+pr+ps+qr+qs+rs)/(\root[3]{3\sqrt(24(pq+pr+ps+qr+qs+rs)^3+81(pqr+qrs+rsp+spq)^2)+27(pqr+qrs+rsp+spq)})<s`
Nhìn đề đến một người theo Toán như anh còn thấy nản í :)
Đúng 5
Bình luận (4)
ừ thì năm nay lên 11 nma toi đ hiểu đây là cgi =))
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
chứng minh rằng tam giác ABC có chu vi 2p ngoại tiếp đường tròn (I ,r )thì diện tích S cửa tam giác có công thức S=p.r
Gọi O là tâm đường tròn nội tiếp tam giác ABC .Nối OA, OB, OC
Nối OA, OB, OC.Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBC.
Ta có:
Mà AB + AC + BC = 2p
Nên
Đúng 1
Bình luận (1)
Gọi I,E,F lần lược là tiếp điểm của đường tròn tâm O nội tiếp với AB,BC,CA
Ta có OI = OE = OF = r
S ABC = S AOB + S BOC + S COA = AB.OI/2 + BC.OE/2 + CA.OF/2 = (AB + BC + CA).r/2 = pr
Đúng 0
Bình luận (0)
so sánh 2^99 với 3^999
dấu ^: mũ
chứng minh có công thức dàng hoàng, không nói kết quả khi không có công thức
Ta có:
2 < 3 ; 99 < 999
=> 299 < 3999
Đúng 0
Bình luận (0)
Tick cho người trả lời đúng nhất
Chứng minh công thức : v02= 2gh
* Lưu ý: Chọn chiều dương là chiều từ trên xuống không phải là chiều từ dưới lên
* Gợi ý: Liên hệ công thức s= v0t+1/2at2
Giờ này không còn ai trả lời đâu chị ạ, còn mỗi chị em mình ;-;
Đúng 0
Bình luận (2)
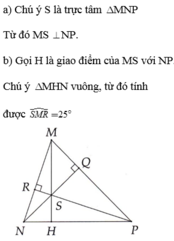
Cho tam giác MNP có ba góc nhọn, các đường cao NQ, PR cắt nhau tại S.
a) Chứng minh M S ⊥ N P .
b) Cho M N P ^ = 45 ° . Tính S M R ^ .
Chứng minh rằng nếu tam giác ABC có chu vi 2p, bán kính đường tròn nội tiếp bằng r thì diện tích S của tam giác có công thức : S = p.r
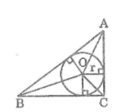
Gọi O là tâm đường tròn nội tiếp tam giác ABC
Nối OA, OB, OC
Khoảng cách từ tâm O đến các tiếp điểm là đường cao của các tam giác OAB, OAC, OBCv
Ta có : S A B C = S O A B + S O A C + S O B C
= (1/2).AB.r + (1/2).AC.r + (1/2).BC.r
= (1/2)(AB + AC + BC).r
Mà AB + AC + BC = 2p
Nên S A B C = (1/2).2p.r = p.r
Đúng 0
Bình luận (0)