Hỏi có bao nhiêu giá trị m nguyên trong đoạn [0; 2017] để phương trình x 2 - 4 x - 5 - m = 0 có hai nghiệm phân biệt?
A. 2016
B. 2008
C. 2009
D. 2017
Trong tập các số phức, cho phương trình z 2 - 4 z + m - 2 2 = 0 , m ∈ ℝ 1 Gọi m 0 là một giá trị của m để phương trình (1) có hai nghiệm phân biệt z 1 , z 2 thỏa mãn . Hỏi trong đoạn z 1 = z 2 có bao nhiêu giá trị nguyên của ?
A. 2019
B. 2015
C. 2014
D. 2018
Hỏi có bao nhiêu giá trị nguyên của tham số thực m để phương trình logarit log 3 2 x + log 3 2 x + 1 - 2 m - 1 = 0 có nghiệm thuộc đoạn 1 ; 3 3
A. 3
B. 2
C. 1
D. 0
Chọn A.
Đặt ![]() . Với
. Với ![]() suy ra 1 ≤ t ≤ 2.
suy ra 1 ≤ t ≤ 2.
Phương trình đã cho trở thành t2 + t = 2m + 2 (*)
Phương trình đã cho có nghiệm thuộc đoạn ![]() có nghiệm 1 ≤ t ≤ 2
có nghiệm 1 ≤ t ≤ 2
Xét hàm số f(t) = t2 + t với1 ≤ t ≤ 2 , ta thấy f’(t) = 2t + 1 nên f(t) là hàm đồng biến trên đoạn [1; 2]
Suy ra 2 = f(1) ≤ f(t) ≤ f(2) = 6
Vậy phương trình có nghiệm khi 2 ≤ 2m + 2 ≤ 6 hay 0 ≤ m ≤ 2
Suy ra có 3 giá trị nguyên m thỏa mãn yêu cầu bài toán.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = 1 3 x 3 - m x 2 + ( m + 2 ) x có hai điểm cực trị nằm trong khoảng 0 ; + ∞ .
A. 2015
B. 2016
C. 2018
D. 4035
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = 1 3 x 3 - m x 2 + ( m + 2 ) x có hai điểm cực trị nằm trong khoảng 0 ; + ∞ .
A. 2015
B. 2016
C. 2018
D. 4035
Chọn B
Phương pháp:
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Ta sử dụng phương trình ![]() có hai nghiệm dương phân biệt
có hai nghiệm dương phân biệt
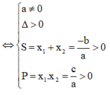
Cách giải:
Ta có ![]()
Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.
Khi đó
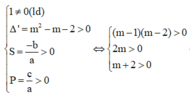
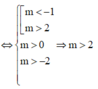
Mà ![]()
![]() nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.
Hỏi có bao nhiêu giá trị mm nguyên trong nửa khoảng (0; 2017] để phương trình | x 2 − 4|x |−5| − m = 0 có hai nghiệm phân biệt?
A. 2016
B. 2008
C. 2009
D. 2017
Hỏi có bao nhiêu giá trị nguyên của m để bất phương trình log 2 2 x + m log 2 x - m ≥ 0 nghiệm đúng với mọi giá trị của x ∈ 0 ; + ∞ ?
A. Có 4 giá trị nguyên
B. Có 6 giá trị nguyên
C. Có 5 giá trị nguyên
D. Có 7 giá trị nguyên
Đáp án C
Đặt t = log 2 x với x ∈ 0 ; + ∞ thì t ∈ ℝ , khi đó bất phương trình trở thành t 2 + m t - m > 0 *
Để (*) nghiệm đúng với mọi t ∈ ℝ ⇔ ∆ * ≤ 0 ⇔ m 2 + 4 m ≤ 0 ⇔ m ∈ - 4 ; 0
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện
Hỏi có bao nhiêu giá trị m nguyên trong đoạn − 2017 ; 2017 để hàm số y = x 3 − 3 2 m + 1 x 2 + 12 m + 5 x − 2 đồng biến trên khoảng 2 ; + ∞ ?
A. 2018
B. 2019
C. 2017
D. 2016
Đáp án A
Để hàm số đồng biến trên khoảng 2 ; + ∞ thì
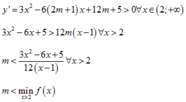
Xét f x = 3 x 2 − 6 x + 5 12 x − 1 có đạo hàm f ' x = 3 x 2 − 6 x + 1 12 x − 1 2 > 0 x > 2
Do đó f(x) đồng biến trên khoảng 2 ; + ∞ hay M i n f x = f 2 = 5 12 ⇒ m < 5 12
Lại có m ∈ − 2017 ; 2017 m ∈ ℤ .
Suy ra có 2018 giá trị của m thỏa mãn
Cho phương trình m − 1 log 1 3 2 x + 1 2 + 4 m − 5 log 1 3 1 x + 1 + 4 m − 4 = 0 1 . Hỏi có bao nhiêu giá trị m nguyên âm để phương trình (1) có nghiệm thực trong đoạn − 2 3 ; 2
A. 6
B. 5
C. 2
D. 3
Đáp án D
Điều kiện: x ∈ − 2 3 ; 2 ⇒ 1 ⇔ 4 m − 1 log 3 x + 1 2 + 4 m − 5 log 3 x + 1 + 4 m − 4 = 0
Đặt t = log 3 x + 1 ⇒ ∈ − 1 ; 1 ⇒ 1 ⇔ m − 1 t 2 + m − 5 t + m − 1 = 0 ⇔ m = t 2 + 5 t + 1 t 2 + t + 1 2
Xét hàm số f t = t 2 + 5 t + 1 t 2 + t + 1 , t ∈ − 1 ; 1 , ta có f ' t = 4 t 2 − 1 t 2 + t + 1 2 ⇒ f ' t = 0 ⇔ t = ± 1
Suy ra f − 1 ≤ f t − 1 ; 1 ≤ f 1 ⇔ − 1 ≤ f t − 1 ; 1 ≤ 7 3 ⇒ 2 ⇔ − 1 ≤ m ≤ 7 3
Suy ra có 3 giá trị nguyên âm của m thỏa đề bài
Hỏi có tất cả bao nhiêu giá trị m nguyên trên đoạn [-2017;2017] để phương trình x 2 − 1 log 2 x 2 + 1 − m 2 x 2 − 1 . log x 2 + 1 + m + 4 = 0 có đúng hai nghiệm x 1 , x 2 thỏa mãn 1 ≤ x 1 ≤ x 2 ≤ 3
A. 4017.
B. 4028.
C. 4012.
D. 4003.