Cho hình chóp S.ABC có S C ⊥ A B C và tam giác ABC vuông tại B. Biết AB=a, A C = a 3 , S C = 2 a 6 . Sin của góc giữa hai mặt phẳng (SAB), (SAC) bằng
A. 2 3
B. 3 13
C. 1
D. 5 7
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A. ; AB = a, AC= a 3 .Tam giác SAB, SAC lần lượt vuông tại B và C. Khối cầu ngoại tiếp hình chóp S.ABC có thể tích bằng 5 5 6 πa 3 . Tính thể tích khối chóp S.ABC
A. a 3 3 3
B. a 3 3 2
C. a 3 3 12
D. a 3 3 6
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=a, AC=2a. Mặt bên (SAB), (SCA) lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 2 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
![]()
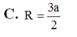
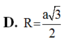
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB = a, AC = 2a. Mặt bên (SAB), (SCA) lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 3 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
A. R = a 2
B. R = a
C. R = 3 a 2
D. R = a 3 2
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Đáp án C
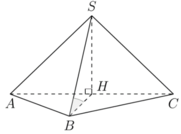
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABC có tam giác ABC vuông tại A, tam giác SAC vuông cân tại S. Biết AB=a, AC=2a, S A C ⊥ A B C . Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
A. 2 πa 2
B. 4 πa 2
C. 5 πa 2
D. 3 πa 2
Cho hình chóp S.ABC có tam giác ABC vuông tại A, tam giác SAC vuông cân tại S. Biết AB = a, Ac = 2a. Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
A. 2 π a 2
B. 4 π a 2
C. 5 π a 2
D. 3 π a 2
Chọn C.
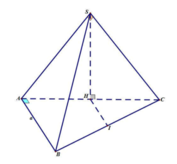
Gọi H, I lần lượt là trung điểm của BC, AC.
Tam giác SAC vuông cân tại S
Tam giác ABC vuông tại A => IA= IB = IC (1).
Lại có:
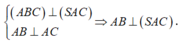
Mà HI là đường trung bình của tam giác ABC
![]()
![]()
![]()
Do đó: I là tâm mặt cầu ngoại tiếp hình chóp S.ABC
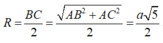
Vậy diện tích mặt cầu là
![]()
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B. Biết ΔSAB là tam giác đều và thuộc mặt phẳng vuông góc với mặt phẳng (ABC). Tính thể tích khối chóp S.ABC biết AB = a, AC = a 3 .
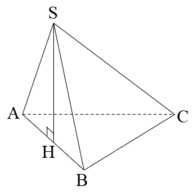
A. a 3 6 12
B. a 3 6 4
C. a 3 2 6
D. a 3 4
Hình chóp S.ABC có đáy ABC là tam giác vuông tại A, AB=a, AC=2a. Mặt bên (SAB), (SCA) lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 3 Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là
![]()
![]()
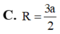
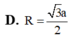
Hình chóp S . A B C có đáy ABC là tam giác vuông tại A , A B = a , A C = 2 a . Mặt bên S A B , S C A lần lượt là các tam giác vuông tại B, C. Biết thể tích khối chóp S.ABC bằng 2 3 a 3 . Bán kính mặt cầu ngoại tiếp hình chóp S . A B C là
A. R = a 2
B. R = a
C. R = 3 a 2
D. R = 3 a 2
Đáp án C

Kẻ hinh chữ nhật A B C D như hình vẽ bên ⇒ S D ⊥ A B C D
Diện tích tam giác ABC là S A B C = 1 2 . A B . A C = a 2
Suy ra V S . A B C = 1 3 . S D . S Δ A B C = a 2 3 . S D = 2 3 a 3 ⇒ S D = 2 a .
Bán kính mặt cầu ngoại tiếp khối chóp S . A B D C là
R = R A B D C 2 + S D 2 4 = a 5 2 2 + 2 a 2 4 = 3 a 2
Vậy bán kính mặt cầu cần tính là R = 3 a 2 .