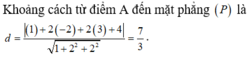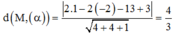Trong mặt phẳng tọa độOxy, cho 3 điểm A(1;0), B(-1;5), C(3;4). Gọi G là trọng tâm của tam giác ABC. Tìm tọa độ điểm G' là ảnh của G qua việc thực hiện liên tiếp phép tịnh tiến theo véc tơ u (2; 3) và phép vị tự tâm C, tỉ số k=-3
TN
Những câu hỏi liên quan
Trong mặt phẳng với hệ tọa độ
Oxy, cho hai điểm A (2;0) , B (6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại điểm A và khoảng cách từ tâm của (C) đến
điểm B bằng 5.
Trong mặt phẳng Oxy, cho hai điểm A(2;0) và B(6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại A và khoảng cách từ tâm của (C) đến B bằng 5.
Gọi I(a;b) là tâm của đường tròn (C).
Vì đường tròn tiếp xúc với trục hoành tại A(2; 0) nên I(2;b) và R = b.
Phương trình đường tròn (C) có dạng: \(\left(x-2\right)^2+\left(y-b\right)^2=b^2\)
Trong mặt phẳng Oxy, cho hai điểm A(2;0) và B(6;4). Viết phương trình đường tròn (C) tiếp xúc với trục hoành tại A và khoảng cách từ tâm của (C) đến B bằng 5.
Gọi I(a;b) là tâm của đường tròn (C).
Vì đường tròn tiếp xúc với trục hoành tại A(2; 0) nên I(2;b) và R = b.
Khoảng cách từ B(6;4) đến tâm I(2;b) bằng 5 nên ta có:
\(IB=5\Rightarrow\sqrt{\left(2-6\right)^2+\left(b-4\right)^2}=5\)
\(\Rightarrow\left(2-6\right)^2+\left(b-4\right)^2=25\)
\(\Rightarrow16+\left(b-4\right)^2=25\)
\(\Rightarrow\left(b-4\right)^2=9\)
\(\Leftrightarrow\left[{}\begin{matrix}b-4=3\\b-4=-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}b=7\\b=-1\end{matrix}\right.\)
Với b = 7, phương trình đường tròn (C) là \(\left(x-2\right)^2+\left(y-7\right)^2=49\)
Với b = 1, phương trình đường tròn (C) là \(\left(x-2\right)^2+\left(y-2\right)^2=1\)
Vậy phương trình đường tròn (C) là \(\left(x-2\right)^2+\left(y-7\right)^2=49\) hoặc \(\left(x-2\right)^2+\left(y-2\right)^2=1\)
Đúng 2
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: A = T v → ( M )
Giả sử A = (x; y). Khi đó

Vậy A = (5; 1)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: M = T v → ( A )
Giả sử A = (x; y). Khi đó

Vậy A = (1; 3)
Đúng 0
Bình luận (0)
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x(1,2), vecto y(3,4), vecto z(5,-1). Tọa độ vecto u 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4...
Đọc tiếp
1. Trong mặt phẳng Oxy, có trọng tâm G(1,-1), M(2,1) và N(4,-2) lần lượt là trung điểm của AB, BC. Tìm tọa độ điểm B
2. Trong mặt phẳng Oxy, cho A(1,3), B(-2,2). Biết đường thẳng AB cắt trục tung tại điểm M(0,b). Giá trị b thuộc khoảng nào
3. Trong mặt phẳng tọa độ Oxy, cho A thỏa vecto OA= 2vecto i + 3vecto j. Tọa độ điểm A là
4. Trong mặt phẳng Oxy, cho vecto x=(1,2), vecto y=(3,4), vecto z=(5,-1). Tọa độ vecto u = 2vecto x + vecto y - vecto z là
5. Trong mặt phẳng tọa độ Oxy, cho M(2,-3), N(4,7). Tọa độ trung điểm I của đoạn thẳng MN là
6. Cho vecto x=(-4,7) và hai vecto a=(2,-1), b=(-3,4). Nếu vecto x = m vecto a + n vecto b thì m, n là cặp số nào
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): x + 2y + 2z + 4 = 0 và điểm A(1;-2; 3). Tính khoảng cách từ điểm A đến mặt phẳng (P).
A. 7 3
B. 2
C. 14 2
D. 1
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng (P): x+ y -z -3 0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 +
2
. Phương trình mặt cầu (S) là A.
x
+
2
2
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;0;-1) và mặt phẳng (P): x+ y -z -3 =0. Mặt cầu (S) có tâm I nằm trên mặt phẳng (P), đi qua điểm A và gốc tọa độ O sao cho chu vi tam giác OIA bằng 6 + 2 . Phương trình mặt cầu (S) là
A. x + 2 2 + y - 2 2 + z + 1 2 = 9 và x + 1 2 + y - 2 2 + z + 2 2 = 9
B. x - 3 2 + y - 3 2 + z - 3 2 = 9 và x - 1 2 + y - 1 2 + z + 1 2 = 9
C. x + 2 2 + y - 2 2 + z - 1 2 = 9 và x 2 + y 2 + z + 3 2 = 9
D. x + 1 2 + y - 2 2 + z + 2 2 = 9 và x - 2 2 + y - 2 2 + z - 1 2 = 9
Đáp án D.
![]()
![]()
![]()
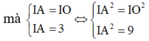
![]()
![]()
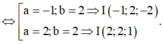
Vậy phương trình mặt cầu cần tìm là
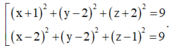
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ oxy cho 3 điểm A(1:1) B(3:2) C(-1:6)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng
α
:
2
x
-
2
y
+
z
-
3
0
và điểm M(1;-2;13). Tính khoảng cách từ điểm M đến mặt phẳng (a).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng α : 2 x - 2 y + z - 3 = 0 và điểm M(1;-2;13). Tính khoảng cách từ điểm M đến mặt phẳng (a).
![]()
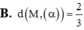
![]()
![]()
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 3) và B(4; 2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B A.
C
−
5
3
;
0
.
B.
C
5
3
;
0
.
C.
C
−...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; 3) và B(4; 2). Tìm tọa độ điểm C thuộc trục hoành sao cho C cách đều hai điểm A và B
A. C − 5 3 ; 0 .
B. C 5 3 ; 0 .
C. C − 3 5 ; 0 .
D. C 3 5 ; 0 .
Ta có C ∈ O x nên C(x, 0) và A C → = x − 1 ; − 3 B C → = x − 4 ; − 2 .
Do C A = C B ⇔ C A 2 = C B 2 .
⇔ x − 1 2 + − 3 2 = x − 4 2 + − 2 2 ⇔ x 2 − 2 x + 1 + 9 = x 2 − 8 x + 16 + 4 ⇔ 6 x = 10 ⇔ x = 5 3 ⇒ C 5 3 ; 0
Chọn B.
Đúng 0
Bình luận (0)