Cho đa thức f(x)=x2+px+q với p;q thuộc Z. Chứng minh rằng tồn tại số nguyên k để f(k)=f(2008).f(2009).
ND
Những câu hỏi liên quan
cho 2 đa thức f(x)=x^2+2mx+m^2 và g(x)=x^2+px+q biết rằng tồn tại x: x2 sao cho f(x1)-g(x1)=0 ; g(x2)-g(x2) = 0 .chứng minh f(x) =g(x), tồn tại x
Mong các bạn giúp đỡ ngày mai mình nộp rồi
Cho hai đa thức K(x)=x2 - 3x +2
L(x)=x2+ px + q + 1
Tìm p,q sao cho K(x) = L(x) với mọi giá trị của x
Nhanh giúp mk nha, mk cảm ơn
\(K\left(x\right)=L\left(x\right)\)
\(\Rightarrow x^2-3x+2=x^2+px+q+1\)
\(\Rightarrow-3x+2=px+q+1\)
-Áp dụng PP hệ số bất định:
\(\Rightarrow p=-3;q+1=2\Rightarrow q=1\)
Đúng 3
Bình luận (0)
Cho hai đa thức:
P
x
-
5
x
3
-
1
3
+
8
x
4
+
x
2
và
Q
x
2
-
5
x
-
3
x
3
+
x...
Đọc tiếp
Cho hai đa thức:
P
x
=
-
5
x
3
-
1
3
+
8
x
4
+
x
2
và Q = x 2 - 5 x - 3 x 3 + x 4 - 2 3
Hãy tính P(x) + Q(x) và P(x) – Q(x).
Sắp xếp hai đa thức theo lũy thừa giảm dần của biến rồi sau đó thực hiện phép tính:

Đúng 0
Bình luận (0)
Cho hai đa thức:
P
x
x
5
-
3
x
2
+
7
x
4
-
9
x
3
+
x
2
-
1
4
x
Q
x
5
x
4
-...
Đọc tiếp
Cho hai đa thức:
P x = x 5 - 3 x 2 + 7 x 4 - 9 x 3 + x 2 - 1 4 x
Q x = 5 x 4 - x 5 + x 2 - 2 x 3 + 3 x 2 - 1 4
Chứng tỏ rằng x = 0 là nghiệm của đa thức P(x) nhưng không phải là nghiệm của đa thức Q(x)
Cho hai đa thức:
P
x
x
5
-
3
x
2
+
7
x
4
-
9
x
3
+
x
2
-
1
4
x
Q
x
5
x
4...
Đọc tiếp
Cho hai đa thức:
P x = x 5 - 3 x 2 + 7 x 4 - 9 x 3 + x 2 - 1 4 x
Q x = 5 x 4 - x 5 + x 2 - 2 x 3 + 3 x 2 - 1 4
Tính P(x) + Q(x) và P(x) – Q(x).
Ta đặt và thực hiện các phép tính P(x) + Q(x) và P(x) – Q(x).

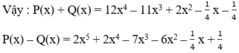
Đúng 0
Bình luận (0)
Cho đa thức f ( x ) = x2 + px + q với \(p\in Z,q\in Z\) . Chứng minh rằng tồn tại số nguyên k để f ( k ) = f ( 2008 ) . f ( 2009 ) .
Cho đa thức \(f(x)\) = \(x^2+px+q\) với p ∈ Z , q ∈ Z. Chứng minh rằng tồn tại số nguyên k để f(k) = \(f(2008).f(2009)\)
Bạn tham khảo lời giải tại đây:
Cho đa thức f(x) = x^2+ax+b(a,b thuộc Z).Chứng minh rằng tồn tại số nguyên tố k để f(x) = f(2019).f(2020) - Hoc24
Đúng 0
Bình luận (0)
Cho g(x) là 1 đa thức với hệ số nguyên. CM: Đa thức f(x)=x2+x.g(x3)f(x)=x2+x.g(x3) không chia hết cho đa thức: x2−x+1
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]f(x)ax4+bx3+cx2+dx+ef(x)ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.Cm đa thức không có nghiệm hữu tỉ2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZCmR các hệ số của P(x) chia hết cho 7.3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)10; P(2)20; P(3)30.Tính P(12)+P(−8)10P(12)+P(−8)104. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)5. Tìm đa thức bậc 3 có hệ số cao...
Đọc tiếp
1. Cho đa thức f(x)ϵZ[x]f(x)ϵZ[x]
f(x)=ax4+bx3+cx2+dx+ef(x)=ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.
Cm đa thức không có nghiệm hữu tỉ
2. Cho P(x) có bậc 3; P(x)ϵZ[x]P(x)ϵZ[x] và P(x) chia hết cho 7 với mọi x ϵZϵZ
CmR các hệ số của P(x) chia hết cho 7.
3. Cho đa thức P(x) bậc 4 có hệ số cao nhất là 1 thỏa mãn P(1)=10; P(2)=20; P(3)=30.
Tính P(12)+P(−8)10P(12)+P(−8)10
4. Tìm đa thức P(x) dạng x5+x4−9x3+ax2+bx+cx5+x4−9x3+ax2+bx+c biết P(x) chia hết cho (x-2)(x+2)(x+3)
5. Tìm đa thức bậc 3 có hệ số cao nhất là 1 sao cho P(1)=1; P(2)=2; P(3)=3
6. Cho đa thức P(x) có bậc 6 có P(x)=P(-1); P(2)=P(-2); P(3)=P(-3). CmR: P(x)=P(-x) với mọi x
7. Cho đa thức P(x)=−x5+x2+1P(x)=−x5+x2+1 có 5 nghiệm. Đặt Q(x)=x2−2.Q(x)=x2−2.
Tính A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5)A=Q(x1).Q(x2).Q(x3).Q(x4).Q(x5) (x1,x2,x3,x4,x5x1,x2,x3,x4,x5 là các nghiệm của P(x))
123456



