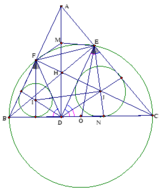
3) Chứng minh EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF

Tứ giác BFEC có  B E C ^ = B F C ^ = 90 0

=> tứ giác BFEC nội tiếp đường tròn đường kính BC

Gọi O là tâm đường tròn ngoại tiếp tứ giác BFEC thì O cũng là tâm đường tròn ngoại tiếp tam giác BEF

∆ OBE cân tại O (do OB=OE) => O B E ^ = O E B ^

∆ AEH vuông tại E có EM là trung tuyến ứng với cạnh huyền AH (Vì M là trung điểm AH)

=> ME=AH:2= MH do đó  ∆ MHE cân tại M=> M E H ^ = M H E ^ = B H D ^

Mà B H D ^ + O B E ^ = 90 0 ( ∆ HBD vuông tại D)

Nên  O E B ^ + M E H ^ = 90 0 Suy ra  M E O ^ = 90 0

⇒ E M ⊥ O E tại E thuộc ( O ) => EM là tiếp tuyến của đường tròn ngoại tiếp tam giác BEF

4) Gọi I và J tương ứng là tâm đường tròn nội tiếp hai tam giác BDF và EDC. Chứng minh DIJ ^   =   DFC ^  

Tứ giác AFDC có A F C ^ = A D C ^ = 90 0  nên tứ giác AFDC nội tiếp đường tròn =>  B D F ^ = B A C ^

∆ BDF và  ∆ BAC có  B D F ^ = B A C ^  (cmt); B ^ chung do đó  ∆ BDF  ~   ∆ BAC(g-g)

Chứng minh tương tự ta có  ∆ DEC ~   ∆ ABC(g-g)

Do đó  ∆ DBF ~ ∆ DEC  ⇒ B D F ^ = E D C ^ ⇒ B D I ^ = I D F ^ = E D J ^ = J D C ^ ⇒ I D J ^ = F D C ^ (1)

Vì  ∆ DBF ~ ∆ DEC (cmt); DI là phân giác, DJ là phân giác  ⇒ D I D F = D J D C  (2)

Từ (1) và (2) suy ra  ∆ DIJ ~ ∆ DFC (c-g-c) =>  DIJ ^   =   DFC ^  

xét tam giác ABC có

CF vuông gọc với AB
BE vuông góc với AC 

suy ra AH vuông góc với BC ( đường cao thứ ba )

giúp mình đi mình tích cho

c/m phần nào