Ở dưới là phần hình ảnh nha
làm giúp mình ạ :)

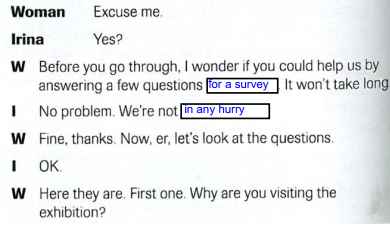
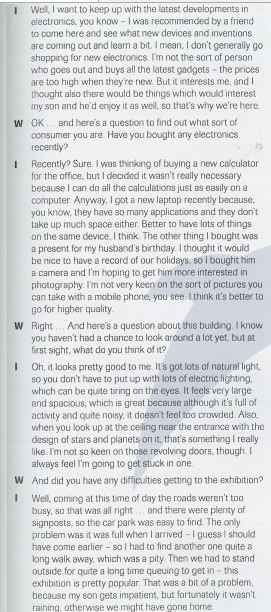
các cao nhân ơi , các cao nhân giúp e với ạ , mọi người chỉ cần làm bài trên ảnh đầu tiên thôi ạ , còn phần bên dưới là script , tại vì mình k có link nghe nên là mk đã cap lại script mọi ng giúp e vs ạ
giúp mình bài 1,2 ở dưới với , có hình ảnh đề bài nha
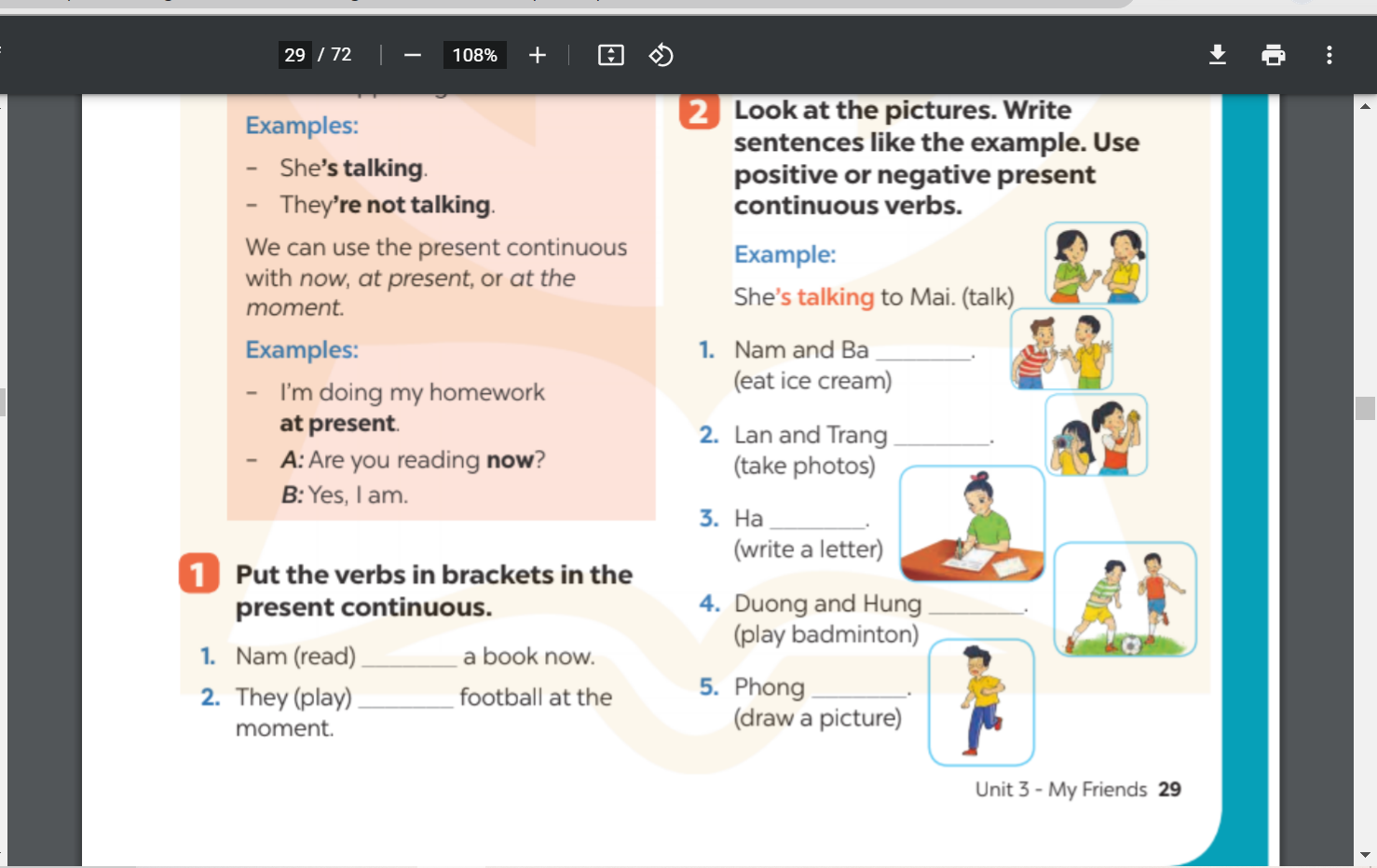 các bạn giúp mình bài 1, bài 2. trang 29 hình ở trên ạ
các bạn giúp mình bài 1, bài 2. trang 29 hình ở trên ạ
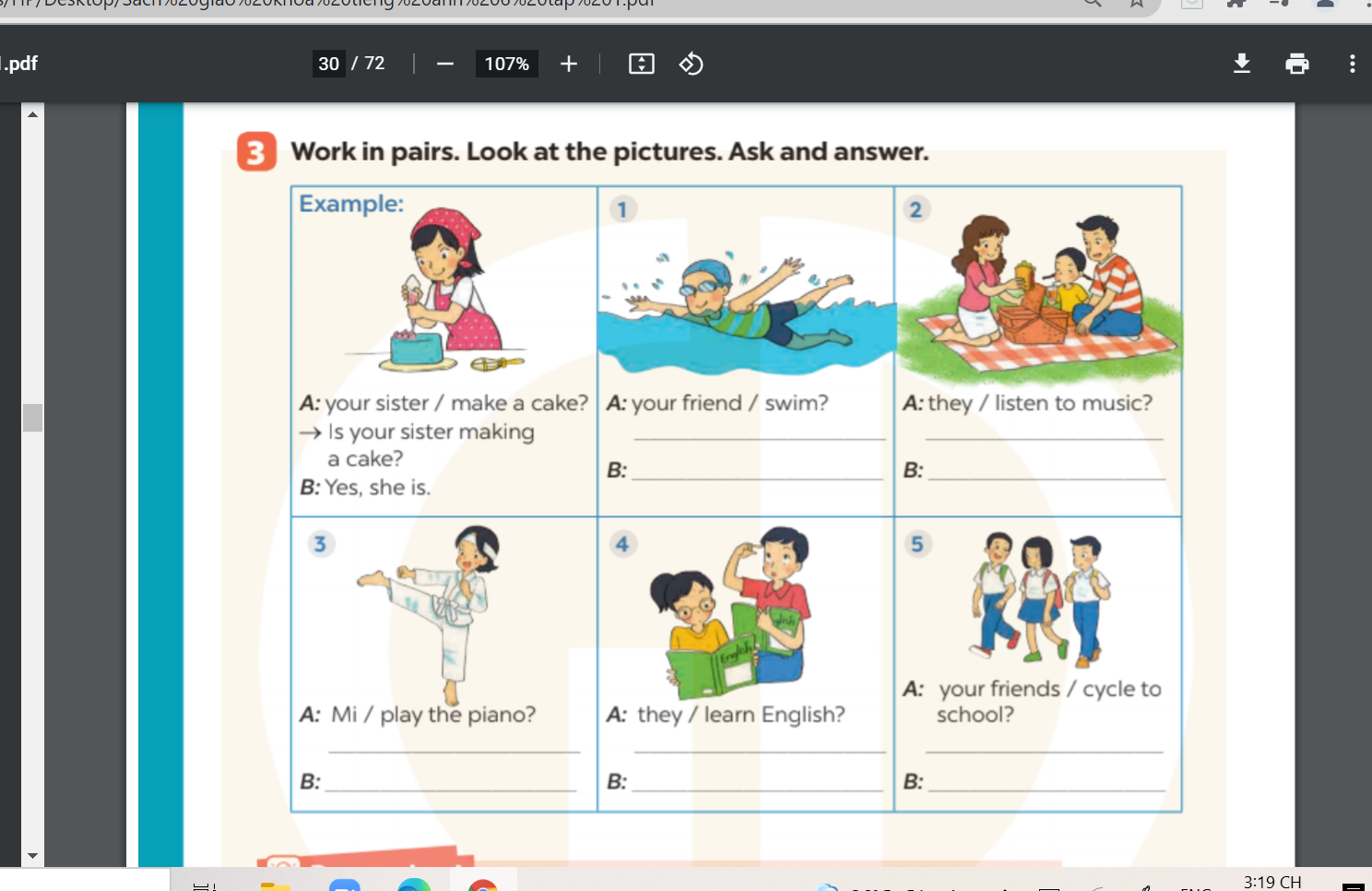 các bạn giúp mình bài 3 hình ở trên đó ạ
các bạn giúp mình bài 3 hình ở trên đó ạ
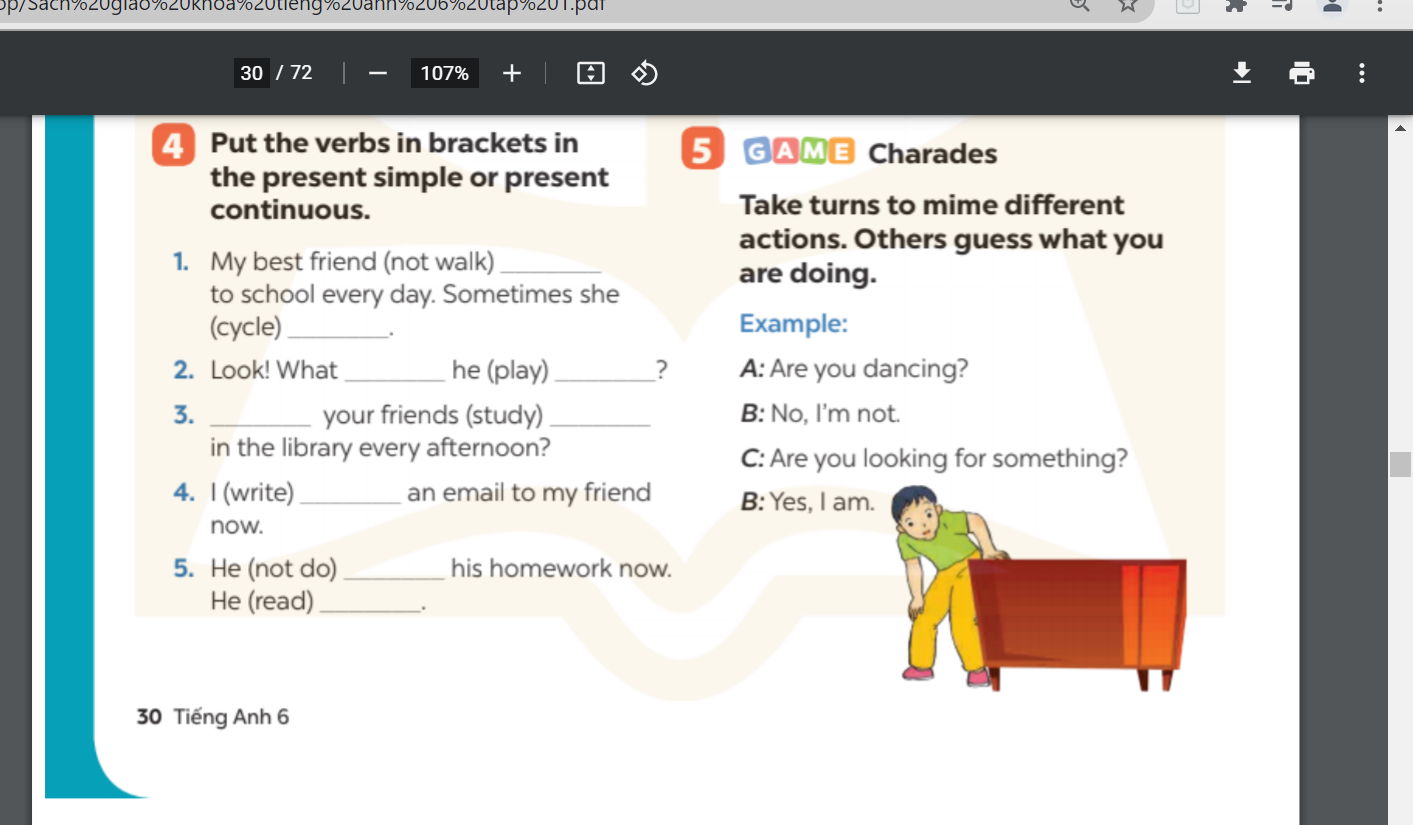
bài 4 hình ảnh ở trên nha mn.
mong mn giúp mình tiếng anh ạ!!! cảm ơn mn ^^
à mình nhầm!!! đó là sách lớp 6 nha mn. ko phải lớp 5 đâu ạ. mong mn giúp !!! ![]()
 Mọi người ơi giúp 2 bài giải có lời giải chi tiết đi ạ ảnh dưới là cách làm mẫu làm ơn giúp mình vì mình đang cần gấp!
Mọi người ơi giúp 2 bài giải có lời giải chi tiết đi ạ ảnh dưới là cách làm mẫu làm ơn giúp mình vì mình đang cần gấp!
Làm báo cáo. Mng giúp mình với ạ. Làm theo như yêu cầu trong ảnh mục || thôi ạ. Nếu trong phần 2 mng không biết có thể tìm trên mạng ạ, nhưng chỉ ghi ý chính thôi nha
Nhìn chung các địa phương Việt Nam đều nuôi những loài gia súc (trâu, bò, lợn, chó, mèo ...), gia cầm (gà, vịt, ngan ...), cá, tôm, ba ba, lươn. Các hình thức nuôi tùy thuộc vào điều kiện của từng gia đinh và từng địa phương. Có trường hợp thì chăn thả để con vật tự kiếm ăn và cho ăn thêm. Có trường hợp nuôi nhốt trong chuồng trại và cung cấp toàn bộ thức ăn cho vật nuôi.
a/ \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt[3]{x^2-1}-2}{x-3}+\lim\limits_{x\rightarrow3}\dfrac{2-\sqrt[4]{1+5x}}{x-3}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x^2-1-8}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{16-1-5x}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4.\sqrt[3]{1+5x}+8\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{-5\left(x-3\right)}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4\sqrt[3]{1+5x}+8\right)}\)
\(=\dfrac{3+3}{\sqrt[3]{\left(3^2-1\right)^2}+2.\sqrt[3]{3^2-1}+4}-\dfrac{5}{\sqrt[4]{\left(1+5.3\right)^3}+2\sqrt[3]{\left(1+5.3\right)^2}+4.\sqrt[3]{1+5.3}+8}=\dfrac{11}{32}\)
\(\Rightarrow a^2+b^2=1145\)
40/
\(L=\lim\limits_{x\rightarrow0}\dfrac{af\left(x\right)+b^n-b^n}{f\left(x\right)\left[\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+....+b^{n-1}\right]}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+...+b^{n-1}}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{b^{n-1}+b^{n-1}++...+b^{n-1}}=\dfrac{a}{nb^{n-1}}\)
40/
\(\sqrt{1+ax}.\sqrt[3]{1+bx}+\sqrt[4]{1+cx}-1=\left(\sqrt{1+ax}-1\right)+\sqrt{1+ax}\left(\sqrt[3]{1+bx}-1\right)+\sqrt{1+ax}.\sqrt[3]{1+bx}.\left(\sqrt[4]{1+cx}-1\right)\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}-1}{x}+\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}\left(\sqrt[3]{1+bx}-1\right)}{x}+\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}.\sqrt[3]{1+bx}\left(\sqrt[4]{1+cx}-1\right)}{x}\)
\(I_1=\lim\limits_{x\rightarrow0}\dfrac{1+ax-1}{x\left(\sqrt{1+ax}+1\right)}=\dfrac{a}{\sqrt{1+ax}+1}=\dfrac{a}{2}\)
\(I_2=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}\left(1+bx-1\right)}{x\left(\sqrt[3]{\left(1+bx\right)^2}+\sqrt[3]{1+bx}+1\right)}=\dfrac{b\sqrt{1+ax}}{\sqrt[3]{\left(1+bx\right)^2+\sqrt[3]{1+bx}+1}}=\dfrac{b}{3}\)
\(I_3=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}\sqrt[3]{1+bx}\left(1+cx-1\right)}{x\left(\sqrt[4]{\left(1+cx\right)^3}+\sqrt[3]{\left(1+cx\right)^2}+\sqrt[3]{1+cx}+1\right)}=\dfrac{c}{4}\)
\(\Rightarrow L=\dfrac{a}{2}+\dfrac{b}{3}+\dfrac{c}{4}\)
P/s: Thông cảm mình đang đau đầu nên làm hơi lâu :b
giúp em phần trắc nghiệm với ạ
ảnh em để ở dưới ạ
Giải giúp mình với! Mình để ảnh bài tập dưới phần bl ạ
Các Bạn không cần làm mà chỉ mình chỗ này mình chưa hiểu : Phần B Khi mà giải ra B = 4/( 3 - căn x) thì làm sao để biết được (3 - căn x) này là âm ạ. Hay cả trên tử cũng vậy (1+căn x) ( liên quan tới hình ảnh bên dưới) 
cái này thì ko nhất thiết phải Cm nha bạn
Câu b kêu tìm x để B ko nhỏ hơn hoặc bằng A
Nghĩa là
\(\dfrac{4}{3-\sqrt{x}}>1\)
\(\Leftrightarrow\dfrac{4}{3-\sqrt{x}}-1>0\)
\(\Leftrightarrow\dfrac{4-\left(3-\sqrt{x}\right)}{3-\sqrt{x}}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}+1}{3-\sqrt{x}}>0\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}+1>0\\3-\sqrt{x}>0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}+1< 0\left(VL\right)\\3-\sqrt{x}< 0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow3-\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}< 3\)
\(\Leftrightarrow x< 9\)
Theo Đk ta có x≥0
Vậy 0≤x<9 thì B ko nhỏ hơn hoặc bằng A
Lời giải giống như bạn dưới đã viết.
Để $B$ không nhỏ hơn hoặc bằng $A$
Tức là $B>A$
$\Leftrightarrow \frac{4}{3-\sqrt{x}}>1$
$\Leftrightarrow \frac{4}{3-\sqrt{x}}-1>0\Leftrightarrow \frac{\sqrt{x}+1}{3-\sqrt{x}}>0$
Để phân thức này dương thì tử và mẫu phải cùng dấu.
Mà $\sqrt{x}+1\geq 0+1>0$ (dương rồi) nên $\sqrt{3}-x$ cũng dương.
------------------------
Đây là cách dễ làm nhất đối với bài này.
------------------------
Về phần lời giải của cô em, chị nghĩ trong lúc giảng em bị miss mất 1 số ý chứ ý cô không phải khẳng định mẫu âm đâu. Có lẽ ý của cô em thế này:
Khi em có: $\frac{4}{3-\sqrt{x}}>1$ thì em không nên nhân chéo mà nên trừ để đưa về hiệu >0 (như bạn Khoa đã giải). Nếu nhân chéo, em sẽ mắc phải 2 TH mẫu âm, mẫu dương như sau:
TH1: $3-\sqrt{x}>0$ thì $\frac{4}{3-\sqrt{x}}>1$ tương đương với $4> 3-\sqrt{x}$
TH2: $3-\sqrt{x}< 0$ thì tương đương $4< 3-\sqrt{x}$ (khi nhân 2 vế với số âm thì phải đổi dấu)
Như vậy thì rất là phức tạp. Nên để tránh TH mẫu âm mà hs giữ nguyên dấu khi nhân chéo thì cô em khuyên như vậy.
Em còn chỗ nào chưa hiểu thì cứ hỏi thoải mái.