tính diện tích hình bên: 3cm 4cm 2cm 2cm 2cm
Đọc tiếp
tính diện tích hình bên:
CM
Những câu hỏi liên quan
Tính diện tích của hình được cho sau đây:
Đa giác ABCDEF, biết AD=4cm, AD=4cm, BC=1cm, FE=2cm, FB=3cm, BC=1cm, FE=2cm, FB=3cm, FB vuông góc với AD như hình
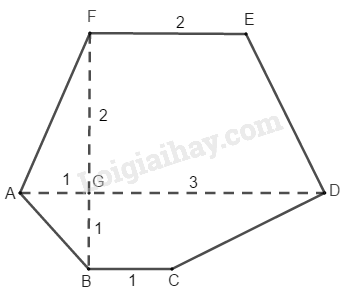
Diện tích đa giác ABCDEF là:
\(S_{ABCDEF}=S_{FGA}+S_{FEDG}+S_{BCDG}+S_{AGB}\\ =\dfrac{2.1}{2}+\dfrac{\left(2+3\right).2}{2}+\dfrac{\left(1+3\right).1}{2}+\dfrac{1.1}{2}\\ =1+5+2+0,5\\ =8,5\left(cm^2\right)\)
Đúng 1
Bình luận (1)
Diện tích của đa giác ABCDEF là :
= \(\dfrac{2.1}{2}\) + \(\dfrac{\left(2+3\right).2}{2}\) + \(\dfrac{\left(1+3\right).1}{2}\) + \(\dfrac{1.1}{2}\)
= 1 + 5 + 2 + 0.5
= 8,5 ( cm2 )
Chúc bạn học tốt nha ❤
Đúng 0
Bình luận (2)
Tính diện tích của hình được cho sau đây:
a Đa giác ABCDEF, biết AD=4cm, AD=4cm, BC=1cm, FE=2cm, FB=3cm, BC=1cm, FE=2cm, FB=3cm, FBFB vuông góc với AD như hình
Tính diện tích của hình được cho sau đây:
Đa giác ABCDEF, biết AD=4cm, AD=4cm, BC=1cm, FE=2cm, FB=3cm, BC=1cm, FE=2cm, FB=3cm, FB vuông góc với AD như hình
Tính diện tích của hình được cho sau đây:
Đa giác ABCDEF, biết AD=4cm, AD=4cm, BC=1cm, FE=2cm, FB=3cm, BC=1cm, FE=2cm, FB=3cm, FB vuông góc với AD như hình
Tính diện tích của hình được cho sau đây:
Đa giác ABCDEF, biết AD=4cm, AD=4cm, BC=1cm, FE=2cm, FB=3cm, BC=1cm, FE=2cm, FB=3cm, FB vuông góc với AD như hình
Tính diện tích của hình được cho sau đây:
Đa giác ABCDEF, biết AD=4cm, AD=4cm, BC=1cm, FE=2cm, FB=3cm, BC=1cm, FE=2cm, FB=3cm, FB vuông góc với AD như hình
cho hình bên biết:
AC=5cm,DC=4cm,AD=3cm,BH=2cm.
a)Tính diện tích tứ giác ABCD.
b)Tính diện tích phần tô màu.
dap an la 20
đáp án là 20
Xem thêm câu trả lời
Tính diện tích của hình bên dưới biết: AG 4cm; GE 2cm; ED 2cm; CD 1cm.
A B C D E G
Đọc tiếp
Tính diện tích của hình bên dưới biết: AG = 4cm; GE = 2cm; ED = 2cm; CD = 1cm.
Diện tích hình trên:
1 x 2+ (2+1) x 4 = 2 + 12 = 14(cm2)
Đ,số: 14cm2
Đúng 0
Bình luận (0)
Đa giác ABCDEF, biết AD=4cm, AD=4cm, BC=1cm, FE=2cm, FB=3cm, BC=1cm, FE=2cm, FB=3cm, FB vuông góc với AD như hình
a) chứng minh rằng ADFE, ABCD là hình thang
b) Tính diện tích của đa giác ABCDEF
Cho đa giác ABCDEF, biết AD=4cm, AD=4cm, BC=1cm, FE=2cm, FB=3cm, BC=1cm, FE=2cm, FB=3cm, FB vuông góc với AD như hình
a) chứng minh rằng ADFE, ABCD là hình thang
b) Tính diện tích của đa giác ABCDEF