Cho hình thang ABCD có A=120, B=2C. C/m hình thang ABCD là hình thang cân
VG
Những câu hỏi liên quan
Cho hình thang cân ABCD (AB // CD) có A ^ = 2 C ^ . Tính các góc của hình thang cân
Ta có A ^ + D ^ = 180 0 , A ^ = 2 C ^ = 2 D ^
Suy ra C ^ = D ^ = 60 0 , A ^ = B ^ = 120 0
Đúng 0
Bình luận (0)
1.Cho tứ giác ABCD có A=120,B=90C=2D
TÍNH C VÀ D
2 .Chi hình thang cân ABCD có AB//CD O là giao điểm của 2đường chéo. CMR:OA=OB, OC=OD
3.Cho hình thang ABCD có
A-D=40, A=2C. Tính A, B, C, D
4. CHO hình thang cân ABCD có
AB//CD AB<CD
CMR DH=CK
Đề bài 4 là :
Cho hình thang cân ABCD(AB//CD , AB<CD), kể đuòng cao AH và BK
CMR: DH=CK
Đúng 0
Bình luận (0)
1)Cho hình thang cân ABCD (AB//DC) có B=2C. Tính B,C,D
2)Cho hình thang cân ABCD (AB//DC) O là giao điểm hai đường chéo AC và BD. Chứng minh OA=ob VÀ oc=op
3)Cho tứ giác ABCD (AB nhỏ hơn DC) AH vuông BC. gọi M,N,I lần lượt là trung điểm AC,AC,BC. chứng minh:
a) MN là đường trung trực của AH
b) Chứng minh tứ giác MHIN là hình thang cân
Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:
a) ΔBDE là tam giác cân.
b) ΔACD = ΔBDC
c) Hình thang ABCD là hình thang cân.
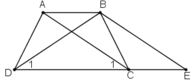
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó ΔBDE cân

Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Đúng 0
Bình luận (0)
Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng: a) ΔBDE là tam giác cân. b) ΔACD = ΔBDC c) Hình thang ABCD là hình thang cân.
a) Hình thang ABEC (AB//CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\) cân
b ) Ta có : AC // BE
\(\Rightarrow\widehat{C}_1=\widehat{E}\) ( 3 )
Tam giác BDE cân tại B ( câu a ) nên \(\widehat{D}_1=\widehat{E}\) ( 4 )
Từ (3 ) và ( 4 ) \(\Rightarrow\widehat{C}_1=\widehat{D}_1\)
Xét \(\Delta ACD\) và \(\Delta BCD\) có AC = CD ( gt )
\(\widehat{C}_1=\widehat{D}_1\left(cmt\right)\)
CD là cạnh chung
Nên \(\Delta ACD=\Delta BCD\left(c.g.c\right)\)
c ) Vì \(\Delta ACD=\Delta BCD\) ( câu b ) \(\Rightarrow\widehat{ADC}=\widehat{BCD}\)
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
1) Chứng minh định lí “Hình thang có hai đường chéo bằng nhau là hình thang cân” qua bài toán sau : Cho hình thang ABCD(AB//CD)ABCD(AB//CD) có AC=BDAC=BD. Qua BB kẻ đường thẳng song song với ACAC, cắt đường thẳng DCDC tại EE. Chứng minh rằng:
a) BDEBDE là tam giác cân.
b) △ACD=△BDC.△ACD=△BDC.
c) Hình thang ABCDABCD là hình thang cân.
chúc hok tốt , k nha! sai cũng k
Cho hình thang ABCD có đáy là AD , A-B = 20 , A=2C . Tính số đo các góc của hình thang ABCD
cho hình thang cân ABCD ( AB//CD) có Góc A = 2C . tính các số đo các gcs của hình thang
Cho hình thang ABCD ( AB//CD). Gọi M;N;P;Q theo thứ tự là trung điểm của các cạnh AB;AC;CD;BD.
a/ Tứ giác MNPQ là hình gì?
b/ Tìm điều kiện của hình thang ABCD để MNPQ là hình thoi?
c/ Khi ABCD là hình thang cân có hai đường chéo vuông góc thì MNPQ là hình gì?
a / hình bình hành
b/ AC=BD ; AB>CD ; AB<AC<CD;AB<BD<CD
c/hình vuông
Đúng 0
Bình luận (0)
(Hình thì bạn tự vẽ nha)
a) Xét tam giác BAD có: MB=MA ; QB=QD
=> MQ là đường trung bình của tam giác BAD
=> MQ // AD ; MQ = 1/2 AD (1)
Xét tam giác CAD có: NC = NA ; PC = PD
=> NP là đường trung bình của tam giác CAD
=> NP // AD ; NP = 1/2 AD (2)
Từ (1), (2) => MQ // NP ; MQ = NP
Tứ giác MNPQ có: MQ // NP ; MQ = NP
=> MNPQ là hình bình hành
b) Theo a), ta có: MQ = 1/2 AD (*)
Xét tam giác ABC có: MA = MB ; NA = NC
=>MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC (**)
Từ (*), (**) và AD=BC (ABCD là thang cân)
=> MQ = MN
Hình bình hành MNPQ có MQ = MN
=> MNPQ là hình thoi
Đúng 0
Bình luận (0)
Do AI, DI lần lượt là phân giác BADˆ;ADCˆ→IADˆ=BADˆ2 và IDAˆ=ADCˆ2
Ta có AIDˆ=180o−(IADˆ+IDAˆ)=180o−BADˆ+ADCˆ2=180o−180o2=90o
Xét Δ AID vuông tại I có IM là trung tuyến thuộc cạnh huyền AD MA=MI
=> Δ AMI cân tại M => MAIˆ=MIAˆ
Do MAIˆ=BAIˆ→BAIˆ=MIAˆ
Mà 2 góc ở vị trí so le trong MI // AB (1)
Tương tự có NJ // AB (2)
Lại có MN // AB (3) ( MN là đường trung bình của hình thang ABCD )
Từ (1); (2) và (3)=> M, N, I, J thẳng hàng.
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho hình thang ABCD, có góc A - góc D bằng 30 độ ; góc B bằng 105 độ
a) tính các góc của hình thang
b) chứng minh hình thang ABCD là hình thang cân


