xét tính đúng sai của mệnh đề:
bất phương trình \(\sqrt{x^2-9x}>1\) có nghiệm
Phát biểu mệnh đề phủ định của mệnh đề K: " Bất phương trình x 2013 > 2030 vô nghiệm " và xét tính đúng sai của nó.
A. K ¯ : “Bất phương trình x 2013 < 2030 có nghiệm”, mệnh đề này đúng
B. K ¯ : “Bất phương trình x 2013 > 2030 vô nghiệm”, mệnh đề này đúng
C. K ¯ : “Bất phương trình x 2013 < 2030 có nghiệm”, mệnh đề này sai
D. K ¯ : “Bất phương trình x 2013 > 2030 có nghiệm”, mệnh đề này đúng
Phát biểu mệnh đề phủ định của mỗi mệnh đề sau và xác định tính đúng sai của mệnh đề phủ định đó.
P: “2 022 chia hết cho 5”
Q: “Bất phương trình 2x + 1 > 0 có nghiệm”.
Mệnh đề phủ định của mệnh đề P là \(\overline P \): “2 022 không chia hết cho 5”
Mệnh đề \(\overline P \) đúng.
Mệnh đề phủ định của mệnh đề Q là \(\overline Q \): “Bất phương trình \(2x + 1 > 0\) vô nghiệm”.
Mệnh đề \(\overline Q \) sai vì bất phương trình \(2x + 1 > 0\) có nghiệm, chẳng hạn: \(x = 0;\;x = 1\).
Xét tính đúng sai của mỗi mệnh đề sau và phát biểu phủ định của nó x =2 là một nghiệm của phương trình x 2 - 4 x - 2 = 0
Mệnh đề sai.
Phủ định là "x = 2 không là nghiệm của phương trình" 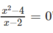 mệnh đề này đúng.
mệnh đề này đúng.
Xét tính đúng sai của mỗi mệnh đề sau và phát biểu phủ định của nó. x =2 là một nghiệm của phương trình x 2 - 4 x - 2 = 0
Mệnh đề sai.
Phủ định là "x = 2 không là nghiệm của phương trình" 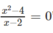 mệnh đề này đúng.
mệnh đề này đúng.
Cho hệ bất phương trình x - 7 ≤ 0 mx ≥ m + 1
Xét các mệnh đề sau :
(1) : Với m< 0 , hệ luôn có nghiệm.
(2) : Với 0 ≤ m < 1/6 hệ vô nghiệm.
(3) : Với m = 1/6 hệ có nghiệm duy nhất.
Mệnh đề nào đúng?
A. Chỉ (1)
B. (2) và (3)
C. Chỉ (3)
D. (1) ; (2) và (3)
Cho hệ bất phương trình x - 7 ≤ 0 m x ≥ m + 1 . Xét các mệnh đề sau
(1) Với m< 0 , hệ luôn có nghiệm.
(2) Với 0 ≤ m < 1/6 hệ vô nghiệm.
(3) Với m= 1/6 , hệ có nghiệm duy nhất.
Mệnh đề nào đúng?
A. Chỉ (1)
B. (2) và (3)
C. Chỉ (3)
D . Cả ba đúng
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R
(III) Khi m≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là 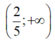
(IV) Khi m> 0 thì hệ bất phương trình đã cho có tập nghiệm là 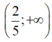
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3
Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó.
a) A: “\(\frac{5}{{1,2}}\) là một phân số”.
b) B: “Phương trình \({x^2} + 3x + 2 = 0\) có nghiệm”.
c) C: “\({2^2} + {2^3} = {2^{2 + 3}}\)”.
d) D: “Số 2 025 chia hết cho 15”.
a) \(\overline A \): “\(\frac{5}{{1,2}}\) không là một phân số”.
Đúng vì \(\frac{5}{{1,2}}\) không là phân số (do 1,2 không là số nguyên)
b) \(\overline B \): “Phương trình \({x^2} + 3x + 2 = 0\) vô nghiệm”.
Sai vì phương trình \({x^2} + 3x + 2 = 0\) có hai nghiệm là \(x = - 1\) và \(x = - 2\).
c) \(\overline C \): “\({2^2} + {2^3} \ne {2^{2 + 3}}\)”.
Đúng vì \({2^2} + {2^3} = 12 \ne 32 = {2^{2 + 3}}\).
d) \(\overline D \): “Số 2 025 không chia hết cho 15”.
Sai vì 2025 = 15. 135, chia hết cho 15.
Cho hệ bất phương trình mx + 2 m > 0 2 x + 3 5 > 1 - 3 x 5
Xét các mệnh đề sau:
(I) Khi m< 0 thì hệ bất phương trình đã cho vô nghiệm.
(II) Khi m= 0 thì hệ bất phương trình đã cho có tập nghiệm là R.
(III) Khi m ≥ 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
(IV) Khi m > 0 thì hệ bất phương trình đã cho có tập nghiệm là 2 5 ; + ∞
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng ?
A. 1
B. 0
C. 2
D. 3