công thức tính của thấu kính hội tụ khi d < f
MV
Những câu hỏi liên quan
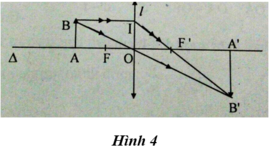
Dựng ảnh của vật tạo bởi thấu kính hội tụ có tiêu cự f = 4cm, khoảng cách từ vật đến thấu kính bằng 8cm.
Chứng minh: d’ = d; h’ = h, lập công thức: f = (d+d')/4
Ta có BI = AO = 2f = 2OF’ => OF’ là đường trung bình của ∆B’BI
=> OB’ = OB => ∆A’B’O = ∆ABO => OA’ = OA = 2f và A’B’ = AB
D = d’ = 2f => d + d’ = 4f => f =(d+d')/4
Đúng 0
Bình luận (0)
1. Thấu kính hội tụ có tiêu cự f = 40cm. Vật sáng AB đặt trước thấu kính và cách thấu kính một khoảng là d.
a. Tính độ tụ của kính
b. Khi d = 20cm. Xác định vị trí, tính chất, độ phóng đại của ảnh
c. Thấu kính được giữ cố định, dịch chuyển vật lại gần thấu kính 10cm, thấy ảnh lúc sau cao gấp 4 lần ảnh trước. Xác định d
a) \(D=\dfrac{1}{f}=\dfrac{1}{40}\)
b) Khi d = 20 cm
\(d'=\dfrac{d.f}{d-f}=\dfrac{20.40}{20-40}=-40\left(cm\right)\)
\(k=-\dfrac{d'}{d}=\dfrac{40}{20}=2\)
=> Ảnh ảo, cùng chiều và lớn hơn vật 2 lần.
Đúng 2
Bình luận (0)
Một thấu kính hội tụ có tiêu cự là f 0 không đổi. Gọi d và d lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm O của thấu kính (Hình 5). Ta có công thức: frac{1}{d} + frac{1}{{d}} frac{1}{f} hay d frac{{df}}{{d - f}}.Xét hàm số gleft( d right) frac{{df}}{{d - f}}. Tìm các giới hạn sau đây và giải thích ý nghĩa.a) mathop {lim }limits_{d to {f^ + }} gleft( d right); b) mathop {lim }limits_{d to + infty } gleft( d right).
Đọc tiếp
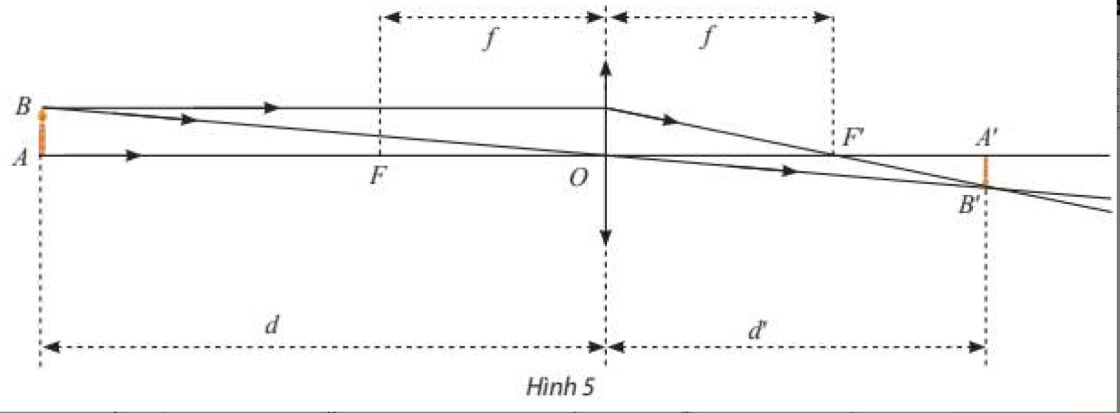
Một thấu kính hội tụ có tiêu cự là \(f > 0\) không đổi. Gọi \(d\) và \(d'\) lần lượt là khoảng cách từ vật thật và ảnh của nó tới quang tâm \(O\) của thấu kính (Hình 5). Ta có công thức: \(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\) hay \(d' = \frac{{df}}{{d - f}}\).
Xét hàm số \(g\left( d \right) = \frac{{df}}{{d - f}}\). Tìm các giới hạn sau đây và giải thích ý nghĩa.
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right)\);
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right)\).
a) \(\mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right).\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}}\)
Ta có: \(\mathop {\lim }\limits_{d \to {f^ + }} \left( {df} \right) = f\mathop {\lim }\limits_{d \to {f^ + }} d = {f^2};\mathop {\lim }\limits_{d \to {f^ + }} \frac{1}{{d - f}} = + \infty \)
\( \Rightarrow \mathop {\lim }\limits_{d \to {f^ + }} g\left( d \right) = \mathop {\lim }\limits_{d \to {f^ + }} \frac{{df}}{{d - f}} = + \infty \)
Ý nghĩa: Khi vật dần đến tiêu điểm từ phía xa thấu kính đến gần thấu kính thì khoảng cách từ ảnh đến thấu kính dần đến \( + \infty \).
b) \(\mathop {\lim }\limits_{d \to + \infty } g\left( d \right) = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d - f}} = \mathop {\lim }\limits_{d \to + \infty } \frac{{df}}{{d\left( {1 - \frac{f}{d}} \right)}} = \mathop {\lim }\limits_{d \to + \infty } \frac{f}{{1 - \frac{f}{d}}} = \frac{f}{{1 - 0}} = f\)
Ý nghĩa: Khi khoảng cách từ vật đến thấu kính càng xa thì ảnh tiến dần đến tiêu điểm của ảnh \(\left( {F'} \right)\).
Đúng 0
Bình luận (0)
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f. Khi 0 d f, ảnh của vật qua thấu kính là A. ảnh thật, cùng chiều và lớn hơn vật B. ảnh ảo, cùng chiều và nhỏ hơn vật C. ảnh ảo, cùng chiều và lớn hơn vật D. ảnh thật, cùng chiều và nhỏ hơn vật
Đọc tiếp
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f. Khi 0 < d < f, ảnh của vật qua thấu kính là
A. ảnh thật, cùng chiều và lớn hơn vật
B. ảnh ảo, cùng chiều và nhỏ hơn vật
C. ảnh ảo, cùng chiều và lớn hơn vật
D. ảnh thật, cùng chiều và nhỏ hơn vật
Đáp án C
Khi 0 < d < f, vật ở trong đoạn FO
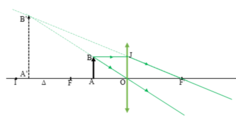
Ảnh là ảo, cùng chiều, lớn hơn vật và nằm ngoài khoảng OF.
Đúng 0
Bình luận (0)
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự fKhi f d 2f, ảnh của vật qua thấu kính là? A. Ảnh thật, ngược chiều và lớn hơn vật B. Ảnh ảo, cùng chiều và nhỏ hơn vật C. Ảnh ảo, ngược chiều và nhỏ hơn vật D. Ảnh thật, cùng chiều và nhỏ hơn vật.
Đọc tiếp
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f
Khi f < d < 2f, ảnh của vật qua thấu kính là?
A. Ảnh thật, ngược chiều và lớn hơn vật
B. Ảnh ảo, cùng chiều và nhỏ hơn vật
C. Ảnh ảo, ngược chiều và nhỏ hơn vật
D. Ảnh thật, cùng chiều và nhỏ hơn vật.
Đáp án: A
Khi f < d < 2f, vật ở trong đoạn FI (hình vẽ)
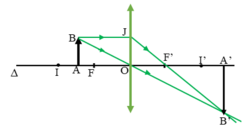
Ảnh thật, ngược chiều, lớn hơn vật và nằm ngoài khoảng OI’.
Đúng 0
Bình luận (0)
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f. Khi f d 2f, ảnh của vật qua thấu kính là A. ảnh thật, ngược chiều và lớn hơn vật B. ảnh ảo, cùng chiều và nhỏ hơn vật C. ảnh ảo, ngược chiều và nhỏ hơn vật D. ảnh thật, cùng chiều và nhỏ hơn vật
Đọc tiếp
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f. Khi f < d < 2f, ảnh của vật qua thấu kính là
A. ảnh thật, ngược chiều và lớn hơn vật
B. ảnh ảo, cùng chiều và nhỏ hơn vật
C. ảnh ảo, ngược chiều và nhỏ hơn vật
D. ảnh thật, cùng chiều và nhỏ hơn vật
Đáp án A
Khi f < d < 2f, vật ở trong đoạn FI
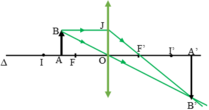
Ảnh thật, ngược chiều, lớn hơn vật và nằm ngoài khoảng OI’
Đúng 0
Bình luận (0)
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f.Khi 0 d f, ảnh của vật qua thấu kính là? A. Ảnh thật, cùng chiều và lớn hơn vật B. Ảnh ảo, cùng chiều và nhỏ hơn vật C. Ảnh ảo, cùng chiều và lớn hơn vật D. Ảnh thật, cùng chiều và nhỏ hơn vật
Đọc tiếp
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f.
Khi 0 < d < f, ảnh của vật qua thấu kính là?
A. Ảnh thật, cùng chiều và lớn hơn vật
B. Ảnh ảo, cùng chiều và nhỏ hơn vật
C. Ảnh ảo, cùng chiều và lớn hơn vật
D. Ảnh thật, cùng chiều và nhỏ hơn vật
Đáp án: C
Khi 0 < d < f, vật ở trong đoạn FO (hình vẽ)
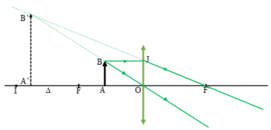
Ảnh là ảo, cùng chiều, lớn hơn vật và nằm ngoài khoảng OF.
Đúng 0
Bình luận (0)
Đặc điểm của thấu kính hội tụ ? Ba tia sáng đặc biệt của thấu kính hội tụ ? Đặc điểm của ảnh của một vật tạo bởi thấu kính hội tụ ? Vẽ ảnh của vật AB tạo bởi TKHT ; nêu đặc điểm ảnh trong các trường hợp : d > 2f ; d = 2f ; f < d < 2f ; d < f
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f. Khi d 2f, ảnh của vật qua thấu kính là A. ảnh thật, cùng chiều và lớn hơn vật B. ảnh ảo, cùng chiều và nhỏ hơn vật C. ảnh ảo, cùng chiều và lớn hơn vật D. ảnh thật, ngược chiều và nhỏ hơn vật
Đọc tiếp
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f. Khi d > 2f, ảnh của vật qua thấu kính là
A. ảnh thật, cùng chiều và lớn hơn vật
B. ảnh ảo, cùng chiều và nhỏ hơn vật
C. ảnh ảo, cùng chiều và lớn hơn vật
D. ảnh thật, ngược chiều và nhỏ hơn vật
Đáp án D
Khi d > f, vật ngoài đoạn OI
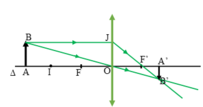
Ảnh là thật, ngược chiều, nhỏ hơn vật
Đúng 0
Bình luận (0)
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f.Khi d 2f, ảnh của vật qua thấu kính là A. Ảnh thật, cùng chiều và lớn hơn vật B. Ảnh ảo, cùng chiều và nhỏ hơn vật C. Ảnh ảo, cùng chiều và lớn hơn vật D. Ảnh thật, ngược chiều và nhỏ hơn vật
Đọc tiếp
Một vật sáng AB đăt vuông góc với trục chính của thấu kính hội tụ. Gọi khoảng cách từ vật đến thấu kính là d, thấu kính có tiêu cự f.
Khi d > 2f, ảnh của vật qua thấu kính là
A. Ảnh thật, cùng chiều và lớn hơn vật
B. Ảnh ảo, cùng chiều và nhỏ hơn vật
C. Ảnh ảo, cùng chiều và lớn hơn vật
D. Ảnh thật, ngược chiều và nhỏ hơn vật
Đáp án: D
Khi d > f, vật ngoài đoạn OI (hình vẽ).
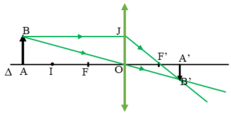
Ảnh là thật, ngược chiều, nhỏ hơn vật.
Đúng 0
Bình luận (0)



