Cho tứ giác ABCD có ^A+^C=60 và AB*CD=AD*BC. Chứng minh: AB*CD=AC*BD
TD
Những câu hỏi liên quan
Cho tứ giác ABCD có \(\widehat{A}+\widehat{C}=60\) và AB*CD=AD*BC. Chứng minh: AB*CD=AC*BD
a)Tứ giác ABCD có AB=CD, AC=BD. Chứng minh ABCD là hình thang cân
b)Tứ giác ABCD có AD=AB=BC và ∠A+∠C=180°. Chứng minh ABCD là hình thang cân
bài 5 : tứ giác abcd có ab+bd< hoặc =ac+cd
chứng minh :ab<ac
bài 6 :cho tứ giác abcd .chứng minh :
a) ab<bc+cd+ad b) ac+bd<ab+bc+cd+ad
cho tứ giác ABCD .chứng minh :
a) AB<BC+CD+AD
b)AC+BD<AB+BC+CD+AD
Cho tứ giác ABCD có
A
^
B
^
và BC AD. Chứng minh:a) ∆DAB ∆CBA, từ đó suy ra BD AC;b)
A
D
C
^
B
C
D
^
;
c) AB // CD
Đọc tiếp
Cho tứ giác ABCD có A ^ = B ^ và BC = AD. Chứng minh:
a) ∆DAB = ∆CBA, từ đó suy ra BD = AC;
b) A D C ^ = B C D ^ ;
c) AB // CD
a) HS tự chứng minh
b) HS tự chứng minh
c) Sử dụng a), b) và tổng bốn góc trong tứ giác
Đúng 0
Bình luận (0)
tứ giác ABCD có AB=CD,BC=AD
a) chứng minh ABCD là hình thang cân
b)cho biết AC vuông góc BD và đường cao AH=4cm.Tính AB+CD
1. Cho hình thang ABCD có góc A góc D 90 độ , đáy nhỏ AB a , cạnh bên BC 2 a . Gọi M , N lần lượt là trung điểm AD , ABa / Tính số đo các góc ABC , BANb/ Chứng minh tam giác NAD đềuc/ Tính MN theo a 2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C 70 độ , góc D 40 độb/ Cho hình thang ABCD có AB // CD và góc A góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 AB^2 + CD^2 + 2AD^23. Cho tứ giác ABCD :a/ Chứng minh rằng AB + CD AC + BDb/ Cho biết AB + B...
Đọc tiếp
1. Cho hình thang ABCD có góc A = góc D = 90 độ , đáy nhỏ AB = a , cạnh bên BC = 2 a . Gọi M , N lần lượt là trung điểm AD , AB
a / Tính số đo các góc ABC , BAN
b/ Chứng minh tam giác NAD đều
c/ Tính MN theo a
2. a/ Tính các góc A , góc B của hình thang ABCD ( AB // CD ) biết góc C = 70 độ , góc D = 40 độ
b/ Cho hình thang ABCD có AB // CD và góc A = góc D . Chứng minh rằng ABCD là hình thang vuông cà AC^2 + BD^2 = AB^2 + CD^2 + 2AD^2
3. Cho tứ giác ABCD :
a/ Chứng minh rằng AB + CD < AC + BD
b/ Cho biết AB + BD < hoặc = AC + CD
Chứng minh rằng AB < AC
4. Cho hình thang ABCD có AC vuông góc BD . CHứng minh rằng :
a/ AB^2 + CD^2 = AD^2 + BC^2
b/ ( AB + CD )^2 = AC^2 + BD^2
bạn hỏi thế này thì chả ai muốn làm -_- dài quá
Đúng 1
Bình luận (0)
Bạn gửi từng câu nhò thì các bạn khác dễ làm hơn!
Đúng 1
Bình luận (0)
dài quà làm sao mà có thòi gian mà trả lời .bạn hỏi ít thoi chứ
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
cho tứ giác ABCD . gọi O là giao điểm của hai đường chéo AC và BD . Chứng minh :
a) AC+BD>AB+CD
b)AC+BD>AD+ BC
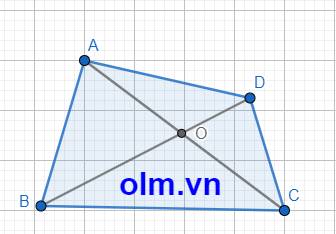
Xét \(\Delta\)AOD ta có: AO + OD > AD (trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Xét \(\Delta\) OCD ta có: BO + OC > BC ( trong 1 tam giác tổng hai cạnh luôn lớn hơn cạnh còn lại)
Cộng vế với vế ta có: AO + OD + BO + OC > AD + BC
(AO + OC) + ( OD + OB > AD + BC
AC+ BD > AD + BC
Chứng Minh tương tự ta có: AC + BD > AB + CD
Đúng 2
Bình luận (0)
Cho hình thang ABCD
(
A
B
/
/
C
D
)
c
ó
A
B
A
D
C
D
/
2
.
Gọi M là trung điểm của CD và H là giao điểm của AM và BD.a) Chứng minh tứ giác ABMD là hình thoib) Chứng minh BD ⊥ BCc) Chứng minh ΔAHD và ΔCBD đồng dạngd) Biết A...
Đọc tiếp
Cho hình thang ABCD ( A B / / C D ) c ó A B = A D = C D / 2 . Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.

a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
![]()
Xét tam giác vuông AHB, ta có :

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
![]()
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)
Đúng 1
Bình luận (0)

