cho a/b+c=b/a+c=c/a+b . tính giá trị của mỗi số hữu tỉ
NS
Những câu hỏi liên quan
Cho 3 số hữu tỉ = nhau là a/b+c,b/c+a,c/a+b .Tìm giá trị của mỗi hữu tỉ số đó .
Giúp mk nka m.n
cho 3 tỉ số a/(b+c)=b/(c+a)/c/(a+b) tìm giá trị mỗi số hữu tỉ
Ta có : \(\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}=\frac{a+b+c}{b+c+c+a+a+b}\)\(=\frac{a+b+c}{2a+2b+2c}=\frac{a+b+c}{2\left(a+b+c\right)}=\frac{1}{2}\)
Vậy \(\frac{a}{b+c}=\frac{b}{c+a}=\frac{c}{a+b}=\frac{1}{2}\)
Đúng 0
Bình luận (0)
Cho a,b,c lad các số hữu tỉ khác 0 sao cho:
Tính giá trị bằng số của mỗi biểu thức: \(M=\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}\)
Cho a, b, c là các số hữu tỉ và khác 0, sao cho a+b+c=0. Tính giá trị của |x|-2019x+2019 biết x= |a|/b+c + |b|/a+c + |c|/a+b.
Cho a/2b+c=b/2c+a=c/2a+b(a,b,c>0). Tính giá trị của mỗi tỉ số .
cho a/2b+c = b/2c+a = c/2a+b ( a,b,c>0). Tính giá trị của mỗi tỉ số
Cho a,b,c là các số hữu tỉ khác 0 thoả mãn : a-b+c/b=b-a+c/a=a-c+b/c . Tính giá trị biểu thứcM=(a+b)(b+c)(c+a)/ abc
Xét \(a+b+c=0\Rightarrow\hept{\begin{cases}a+b=-c\\b+c=-a\\c+a=-b\end{cases}}\Rightarrow M=\frac{\left(-a\right)\left(-b\right)\left(-c\right)}{abc}=-1\)
Xét \(a+b+c\ne0\) ta có:\(\frac{a-b+c}{b}=\frac{b-c+a}{c}=\frac{c-a+b}{a}=\frac{a-b+c+b-c+a+c-a+b}{a+b+c}=1\)
\(\Rightarrow\hept{\begin{cases}a-b+c=b\\b-c+a=c\\c-a+b=a\end{cases}}\Rightarrow\hept{\begin{cases}a+c=2b\\a+b=2c\\b+c=2a\end{cases}}\Rightarrow M=\frac{2a.2b.2c}{abc}=8\)
Đúng 0
Bình luận (0)
Cho
∫
0
1
x
d
x
2
x
+
1
2
a
+
b
ln
2
+
c
ln
3
với a, b, c là các số hữu tỉ. Giá trị của a+b+c bằng A.
1
12...
Đọc tiếp
Cho ∫ 0 1 x d x 2 x + 1 2 = a + b ln 2 + c ln 3 với a, b, c là các số hữu tỉ. Giá trị của a+b+c bằng
A. 1 12
B. 5 12
C. - 1 3
D. 1 4
Cho
∫
0
1
x
d
x
2
x
+
1
2
a
+
b
ln
2
+
c
ln
3
với a, b, c là các số hữu tỉ. Giá trị của
a
+
b
+
c...
Đọc tiếp
Cho ∫ 0 1 x d x 2 x + 1 2 = a + b ln 2 + c ln 3 với a, b, c là các số hữu tỉ. Giá trị của a + b + c bằng:
A. 5 12
B. 1 12
C. − 1 3
D. 1 4
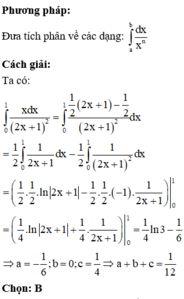
Chú ý: Chú ý khi sử dụng các nguyên hàm mở rộng.
Đúng 0
Bình luận (0)


