Số đuòng chéo xuất phát tù đỉnh của 1 lục giác là
TT
Những câu hỏi liên quan
Số đường chéo xuất phát từ 1 đỉnh của lục giác là ...... đường chéo
Công thức : Số đừng chéo xuất phát từ 1 đỉnh ủa đa giác lồi n cạnh là
n -3
+ lục giác => 6 -3 =3
Đúng 0
Bình luận (0)
Số đường chéo xuất phát từ 1 đỉnh của lục giác là..............đường chéo
Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là?
A. 15
B. 16
C. 17
D. 18
Số đường chéo xuất phát từ 1 đỉnh của đa giác n cạnh là n – 3
Do đó, Số đường chéo xuất phát từ 1 đỉnh của đa giác 20 cạnh là: 20 – 3 = 17
Chọn đáp án C
Đúng 0
Bình luận (0)
một đa giác có tổng số đo của tất cả các góc trong bằng 19800. số đường chéo xuất phát từ 1 đỉnh của đa giác đó là
Lục giác có bao nhiêu đường chéo xuất phát từ một đỉnh?
ai làm được mình tick cho
Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a)
Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b).
Tham khảo:
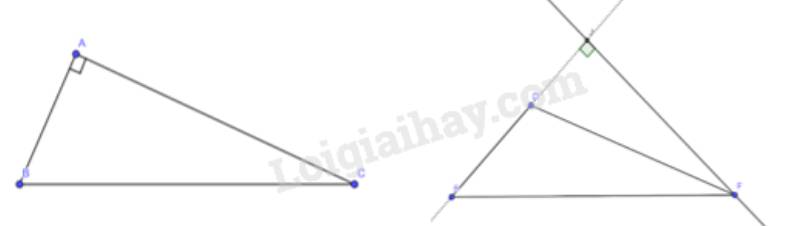
a) Ta thấy ở tam giác ABC vuông tại A thì BA chính là đường cao từ đỉnh B của tam giác vuông ABC
b) Ta thấy đường cao tam giác tù DEF xuất phát từ đỉnh F sẽ nằm ngoài tam giác DEF và chân đường cao nằm trên đoạn kéo dài của đoạn ED.
Đúng 0
Bình luận (0)
cho em hỏi mấy câu này;
1/ công thức tính số đường chéo của đa giác
2/ công thức tính tổng số đo các góc của đa giác
3/ công thức tính số cạnh của đa giác
4/ công thức tính số đường chéo xuất phát từ 1 đỉnh của đa giác
hình như toàn chép bài nhau thì phải
Đúng 0
Bình luận (0)
Gọi n là số cạnh của đa giác.
Ta có :
- Số đường chéo của đa giác là : n(n−3)2
Cái này dễ chứng minh thôi bn!
Từ mỗi đỉnh của hình n giác lồi ta vẽ được n - 1 đoạn thẳng nối đỉnh đó với n - 1 đỉnh còn lại, trong đó có 2 đoạn thẳng trùng với 2 cạnh của đa giác. Vậy qua mỗi đỉnh của hình n giác lồi vẽ được n - 3 đường chéo, hình n giác có n đỉnh nên vẽ được n(n - 3) đường chéo, trong đó mỗi đường chéo được tính 2 lần nên thực chất chỉ có n(n−3)2 đường chéo.
- Tổng số đo các góc trong đa giác : 180o.(n−2)
Còn số cạnh của đa giác thì tự đếm ra, nếu đề bài cho 1 số gt bắt tìm số cạnh thì dựa vào công thức tính đường chéo hay công thức tính số đo 1 góc đa giác đều (180o.(n−2)n.
Số đường chéo xuất phát từ mỗi đỉnh của đa giác n cạnh là n - 3.
__________________
Đúng 0
Bình luận (0)
Số đường chéo xuất phát từ một đỉnh của đa giác ABCDE là bao nhiêu
A,1
B,2
C,3
D,4
Cho một lục giác đều ABCDEF. Viết các chữ cái A, B, C, D, E, F vào sáu cái thẻ. Lấy ngẫu nhiên hai thẻ. Tìm xác suất sao cho đoạn thẳng mà các đầu mút là các điểm được ghi trên hai thẻ đó là:
a. Cạnh của lục giác.
b. Đường chéo của lục giác.
c. Đường chéo nối hai đỉnh đối diện của lục giác.
Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 thẻ trong số 6 thẻ.
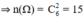
a. Gọi A: “ Hai điểm là đầu mút của cạnh của lục giác”
⇒ n(A) = 6 (Lục giác có 6 cạnh)
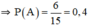
b. Gọi B: “ Hai điểm là đầu mút của đường chéo”
⇒ B = A− (Vì một đoạn thẳng chỉ có thể là một cạnh hoặc một đường chéo)
⇒ P(B) = 1 – P(A) = 1 – 0,4 = 0,6
c. Gọi C: “ Hai điểm là đầu mút của đường chéo nối hai đỉnh đối diện”
⇒ n(C) = 3
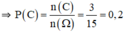
Đúng 0
Bình luận (0)



