Giúp mình 2 bài này mọi người . Cám ơn mọi người

mọi người giúp mình giải 2 bài tập này nhé. cám ơn mọi người rất nhiều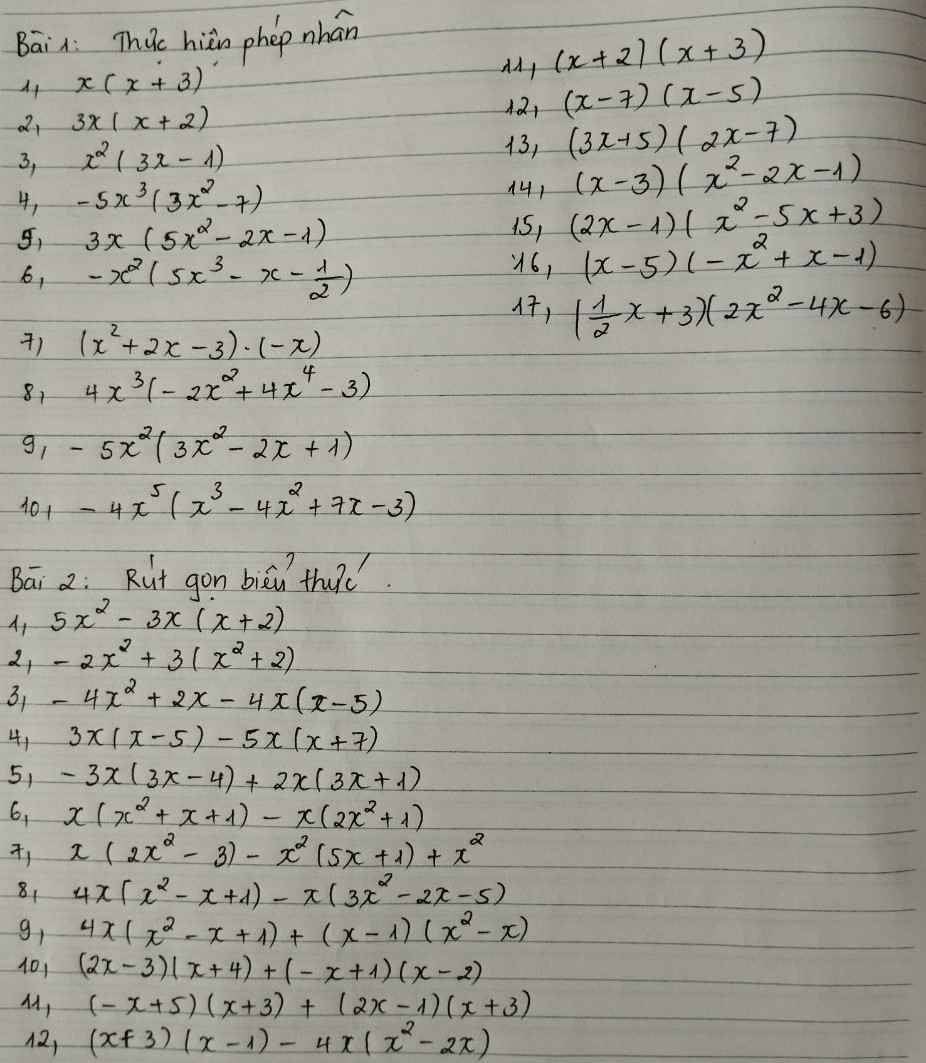
Bài 1
1.\(x\left(x+3\right)\)
\(=x^2+3x\)
2.\(3x\left(x+2\right)\)
\(=3x^2+6x\)
3,\(x^2\left(3x-1\right)\)
\(=3x^3-x^2\)
4.\(-5x^3\left(3x^2-7\right)\)
\(=-15x^5+35x^3\)
5.\(3x\left(5x^2-2x-1\right)\)
\(=15x^3-6x^2-3x\)
6.\(-x^2\left(5x^3-x-\dfrac{1}{2}\right)\)
\(=-5x^5+x^3+\dfrac{x^2}{2}\)
7.\(\left(x^2+2x-3\right).\left(-x\right)\)
\(=-x^3-2x^2+3x\)
8.\(4x^3\left(-2x^2+4x^4-3\right)\)
\(=-8x^5+16x^7-12x^3\)
9.\(-5x^2\left(3x^2-2x+1\right)\)
\(=-15x^4+10x^3-5x^2\)
10.\(-4x^5\left(x^3-4x^2+7x-3\right)\)
\(=-4x^8+16x^7-28x^6+12x^5\)
11.\(\left(x+2\right)\left(x+3\right)\)
\(=x^2+3x+2x+6\)
12.\(\left(x-7\right)\left(x-5\right)\)
\(=x^2-5x-7x+35\)
13.\(\left(3x+5\right)\left(2x-7\right)\)
\(=6x^2-21x+10x-35\)
14.\(\left(x-3\right)\left(x^2-2x-1\right)\)
\(x^3-2x^2-x-3x^2+6x+3\)
15.\(\left(2x-1\right)\left(x^2-5x+3\right)\)
\(=2x^3-10x^2+6x-x^2+5x-3\)
16.\(\left(x-5\right)\left(-x^2+x-1\right)\)
\(=-x^3+x^2-x+5x^2-5x+5\)
17,\(\left(\dfrac{1}{2}x+3\right)\left(2x^2-4x-6\right)\)
\(=x^3-2x^2-3x+6x^2-12x-18\)
P/s:mình làm hơi tắt tại bài dài quá:))
Bài 2
1.\(5x^2-3x\left(x +2\right)\)
\(=5x^2-3x^2+2\)
\(=2x^2+2\)
2.\(-2x^2+3\left(x^2+2\right)\)
\(=-2x^2+3x^2+6\)
\(=x^2+6\)
3.\(-4x^2+2x-4x\left(x-5\right)\)
\(=-4x^2+2x-4x^2+20x\)
\(=22x\)
4.\(3x\left(x-5\right)-5x\left(x+7\right)\)
\(=3x^2-15x-5x^2-35x\)
\(=-2x^2-50x\)
5.\(-3x\left(3x-4\right)+2x\left(3x+1\right)\)
\(=-9x^2+12x+6x^2+2x\)
\(=-3x^2+14x\)
6.\(x\left(x^2+x+1\right)-x\left(2x^2+1\right)\)
\(=x^3+x^2+x-2x^3-x\)
\(=-x^3+x^2\)
7.\(x\left(2x^2-3\right)-x^2\left(5x+1\right)+x^2\)
\(=2x^3-3x-5x^3-x^2+x^2\)
\(=-3x^3-3x\)
8.\(4x\left(x^2-x+1\right)-x\left(3x-2x-5\right)\)
\(=4x^3-4x^2+4x-3x^2+2x^2+5x\)
\(=4x^3-5x^2+9x\)
9.\(4x\left(x^2-x+1\right)+\left(x-1\right)\left(x^2-x\right)\)
\(=4x^3-4x^2+4x+x^3-x^2-x^2+x\)
\(=5x^3-6x^2+5x\)
10.\(\left(2x-3\right)\left(x+4\right)+\left(-x+1\right)\left(x-2\right)\)
\(=2x^2+8x-3x-12+-x^2+2x+x-2\)
\(=x^2+8x-14\)
11.\(\left(-x+5\right)\left(x+3\right)+\left(2x-1\right)\left(x+3\right)\)
\(=-x^2-3x+5x+15+2x^2+6x-x-3\)
\(=x^2+7x+12\)
12.\(\left(x+3\right)\left(x-1\right)-4x\left(x^2-2x\right)\)
\(=x^2-x+3x-3-4x^3+8x^2\)
\(=9x^2+2x-3-4x^3\)
Bài nhiều câu như thế này lần sau bạn lưu ý tách ra các post riêng nhé.
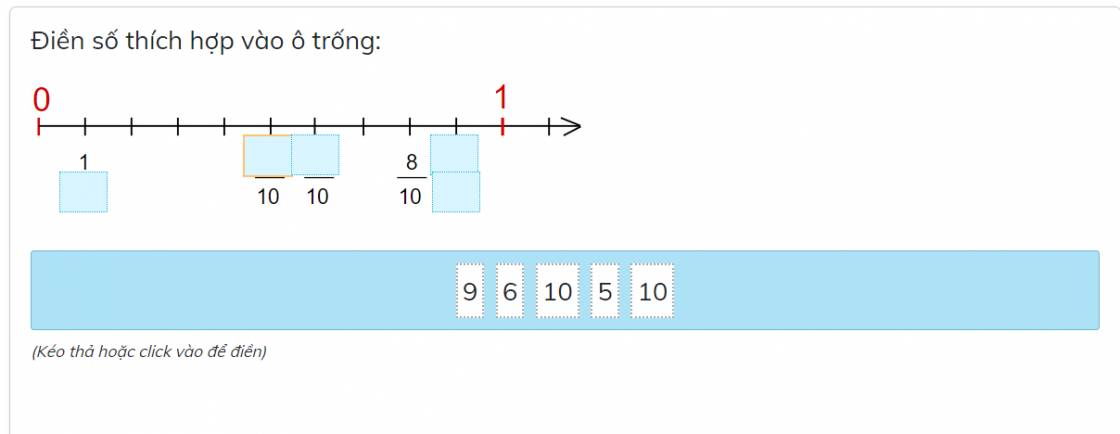 Mọi người giúp mình bài này với ạ!!!
Mọi người giúp mình bài này với ạ!!!
Cám ơn mọi người nhìu ạ!!!!
Từ 0 đến 1 được chia thành 10 phần bằng nhau.
Giá trị của mỗi phần là: \(\dfrac{1}{10}\)
Từ lập luận trên ta có:
Số thích hợp để điền vào các ô trống lần lượt là:
10; 5; 6; 9; 10
0 ; 1/10 ; 2/10 ; 3/10 ; 4/10 ; 5/10 ; 6/10 ; 7/10 ; 8/10 ; 9/10 ; 1
Chúc bạn học tốt!
Mọi người ơi cho mình hỏi 5 câu của bài này . Cám ơn mọi người

Mọi người giúp mình bài này vs
Viết ra thành câu hoàn chỉnh giúp mình nha mình đag cần gấp xin cám ơn
mọi người giúp mình trả lời câu hỏi này với ạ. cám ơn mọi người rất rất nhiều
`7,`
`a, B+A=4x-2x^2+3`
`-> B=(4x-2x^2+3)-A`
`-> B=(4x-2x^2+3)-(x^2-2x+1)`
`B=4x-2x^2+3-x^2+2x-1`
`B=(-2x^2-x^2)+(4x+2x)+(3-1)`
`B=-3x^2+6x+2`
`b, C-A=-x+7`
`-> C=(-x+7)+A`
`-> C=(-x+7)+(x^2-2x+1)`
`-> C=-x+7+x^2-2x+1`
`C=x^2+(-x-2x)+(7+1)`
`C=x^2-3x+8`
`c,`
`A-D=x^2-2`
`-> D= A- (x^2-2)`
`-> D=(x^2-2x+1)-(x^2-2)`
`D=x^2-2x+1-x^2+2`
`D=(x^2-x^2)-2x+(1+2)`
`D=-2x+3`
`6,`
`a,`
`P+Q=4x-2x^2+3`
`-> Q=(4x-2x^2+3)-P`
`-> Q=(4x-2x^2+3)-(3x^2+x-1)`
`Q=4x-2x^2+3-3x^2-x+1`
`Q=(-2x^2-3x^2)+(4x-x)+(3+1)`
`Q=x^2+3x+4`
`b,`
`x^2-5x+2-P=H`
`-> H= (x^2-5x+2)-(3x^2+x-1)`
`H=x^2-5x+2-3x^2-x+1`
`H=(x^2-3x^2)+(-5x-x)+(2+1)`
`H=-4x^2-6x+3`
`c,`
`P-R=5x^2-3x-4`
`-> R= P- (5x^2-3x-4)`
`-> R=(3x^2+x-1)-(5x^2-3x-4)`
`R=3x^2+x-1-5x^2+3x+4`
`R=(3x^2-5x^2)+(x+3x)+(-1+4)`
`R=-2x^2+4x+3`
Giúp mình làm 2 bài này với mọi người cám ơn trước nhaa 
bài 26: gọi quãng đường đi là S
=|> thời gian đi với v1: t1=S/12
thòi gia đi quãng đường với v2 là :t2=S/15
theo đề ta có pt: t1=t2+1
<=>\(\frac{S}{12}=\frac{S}{15}+1\)
<=> \(\frac{S}{60}=1\)
=> S=60km
Nhờ mọi người giải giúp mình bài này .. Cám ơn mọi người ! :)
Tìm x biết:
\(\left(-\frac{3}{4}\right)^x=\frac{81}{256}\)
mọi người ơi giúp mình giải bài toán này với x^3+y^3=(x+y).[(x-y)^3+xy].giải nhanh hộ mình nhé mình cám ơn nhiều
Mình sẽ làm theo đề bài của mình nếu đúng thì ... nha
Biến đổi vế phải ta có :
( x + y) [ ( x - y)^2 + xy ] = ( x + y)( x^2 - 2xy + y^2 + xy)
= ( x+ y)( x^2 - xy+ y^2)
= x^3 + y^3
VẬy VT = VP đẳng thức được CM
hảo thật đấy

Ai giúp mình giải câu này với ạ. Mình cám ơn mọi người nhiều.
Câu nào đấy ạ :)
BÀI TOÁN ĐÂU EM :))
Mọi người làm ơn giúp mình khẩn cấp câu này. Cám ơn mọi người nhiều!!!
Tìm giá trị nhỏ nhất của biểu thức:
\(A=x^2+10y^2+2x-6xy-10y+25\)
\(A=x^2+10y^2+2x-6xy-10y+25\)
=> \(A=x^2+2x\left(1-3y\right)+\left(1-3y\right)^2-\left(1-3y\right)^2-10y+25\)
=> \(A=\left(x+1-3y\right)^2-1+6y-9y^2-10y+25\)
=> \(A=\left(x+1-3y\right)^2-9y^2-4y+24\)
=> \(A=\left(x+1-3y\right)^2-\left(3y\right)^2-2.3y.\frac{2}{3}-\left(\frac{2}{3}\right)^2+\frac{220}{9}\)
=> \(A=\left(x+1-3y\right)^2-\left(3y+\frac{2}{3}\right)^2+\frac{220}{9}\)
Có \(\left(x+1-3y\right)^2\ge0\)với mọi x, y
\(\left(3y+\frac{2}{3}\right)^2\ge0\)với mọi y
=> \(A=\left(x+1-3y\right)^2-\left(3y+\frac{2}{3}\right)^2+\frac{220}{9}\ge\frac{220}{9}\)với mọi x, y
Dấu "=" xảy ra <=> \(\left(x+1-3y\right)^2=0\)<=> \(x+1-3y=0\)
và \(\left(3y+\frac{2}{3}\right)^2=0\)=> \(3y+\frac{2}{3}=0\)
=> \(\hept{\begin{cases}x=\frac{-5}{3}\\y=\frac{-2}{9}\end{cases}}\)
Bổ xung phần kết luận
KL: Amin = \(\frac{220}{9}\)<=> \(\hept{\begin{cases}x=\frac{-5}{3}\\y=\frac{-2}{9}\end{cases}}\)
Bài giải trên nhầm một chỗ
Xét biểu thức sau a - b với b >= 2. Như vậy ta có a - b <= a - 2
Vì vậy nên suy luận có \(\left(x+1-3y\right)^2\ge0\)
và \(\left(3y+\frac{2}{3}\right)^2\ge0\)
sau đó suy ra \(A\ge\frac{220}{9}\)
LÀ SAI
Bạn xem lại bài của mình xem nhé