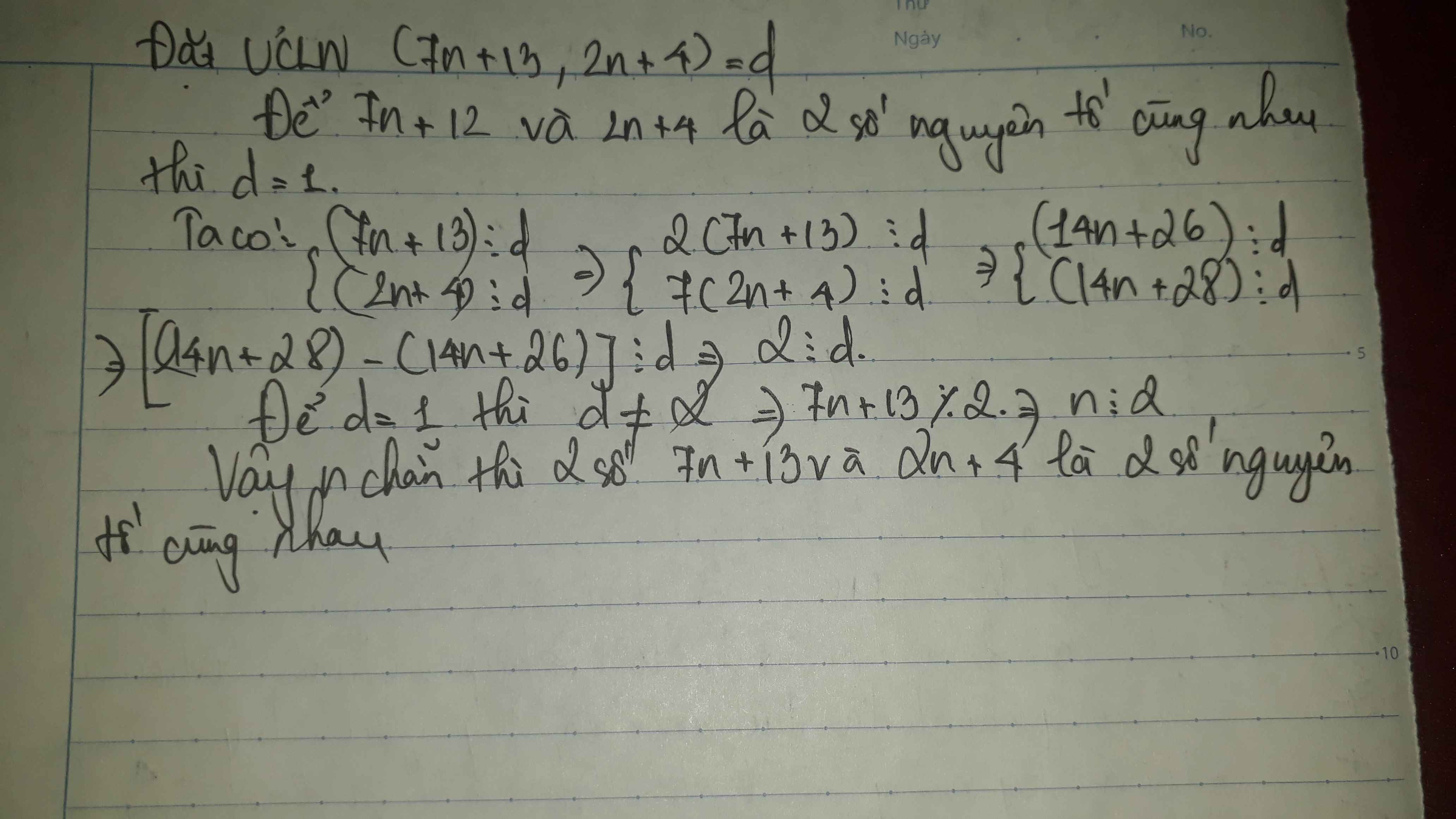Tìm n \(\in\)N để n + 1 và 7n + 4 là hai số nguyên tố cùng nhau
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
H24
Những câu hỏi liên quan
1. Chứng tỏ rằng với n \(\in\)N thìn+1 và 7n+4 là hai số nguyên tố cùng nhau.
2. Tìm n\(\in\)N thì 2n+1 và 4n+1 là hai số nguyên tố cùng nhau.
3. Tìm số nguyên tố p sao cho p+2 và p+4 đều là số nguyên tố.
4. Tìm số tự nhiên n sao cho \(n^2\)+3 là số chính phương.
Tìm n thuộc N để 7n+13 và 2n+4 là hai số nguyên tố cùng nhau?
tìm số tự nhiên n để hai số : 7n+ 13 và 2n+4 là hai số nguyên tố cùng nhau
Tìm ƯCLN của 7n + 3 và 8n - 1 ( \(n\in N\)*)
Khi nào hai số đó Nguyên Tố cùng nhau ? tìm n trong khoảng từ 40 đến 90 để chúng ko nguyên tố cùng nhau.
tim n thuộc N để n + 1 Và 7n + 4 là hai số nguyên tố cùng nhau
Bài này đã đc làm tại link: Câu hỏi của Thái Trần Thảo Vy - Toán lớp 6 - Học toán với OnlineMath
tìm n để 2n 1 và 7n 2 là hai số không
nguyên tố cùng nhau
Xem chi tiết
tìm số tự nhiên n để 2n+1 và 7n+2 là hai số nguyên tố cùng nhau
Để 2n+1 và 7n+2 là hai số nguyên tố cùng nhau
<=> ƯCLN(2n+1;7n+2) = 1
<=> 7.(2n+1)-2.(7n+2) chia hết cho 1
<=> 14n+7-14n-4 chia hết cho 1
<=> 3 chia hết cho 1
Vậy n = 3 (thỏa mãn \(n\in N\) )
Đúng 0
Bình luận (0)
mik thấy câu rả lời này nhiều lắm,chắc các bn copy của nhau chớ gì.mik cần câu trả lời tự làm của các bn nhưng phải chi tiết ,rõ ràng và chính xác
Đúng 0
Bình luận (0)
Gọi \(\left(2n+1;7n+2\right)=d\)
\(\Rightarrow\hept{\begin{cases}2n+1⋮d\\7n+2⋮d\end{cases}\Rightarrow\hept{\begin{cases}14n+7⋮d\\14n+4⋮d\end{cases}\Rightarrow}\left(14n+7\right)-\left(14n+4\right)⋮d}\)
\(\Rightarrow3⋮d\Rightarrow d\in\left\{1;3\right\}\)
\(d=3\Rightarrow2n+1⋮3\Rightarrow4n+2⋮3\Rightarrow3n+n+2⋮3\)
\(\Rightarrow n+2⋮3\Rightarrow n=3k-2\left(k\inℕ^∗\right)\)
=> d=3 thì rút gọn được
\(\Rightarrow n#3k-2\Rightarrow\)tối giản
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm số tự nhiên n để: 2n+1 và 7n+2 là hai số nguyên tố cùng nhau
Tìm số tự nhiên n để 2n+1 và 7n+2 là hai số nguyên tố cùng nhau.
Để 2n + 1 và 7n + 2 nguyên tố cùng nhau
<=> ƯCLN(2n + 1; 7n + 2) = 1
<=> 7.(2n + 1) - 2.(7n + 2) chia hết cho 1
<=> 14n + 7 - 14n + 4 chia hết cho 1
<=> 3 chia hết cho 1
Vậy n = 3
Đúng 1
Bình luận (0)
Xem thêm câu trả lời