Chứng minh rằng trong một tứ giác, tổng độ dài hai đường chéo lớn hơn tổng hai cạnh đối.
NK
Những câu hỏi liên quan
Giúp mình 1 bài này thôi nha :3 (ko spam, sao chép nhá) Chứng minh rằng trong một tứ giác thì: a) Tổng độ dài 2 cạnh đối diện nhỏ hơn tổng độ dài hai đường chéo. b) Tổng độ dài hai đường chéo lớn hơn nửa chu vi của tứ giác.
Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn nửa chu vi tứ giác đó và nhỏ hơn chu vi tứ giác đó:
*Theo câu 1 thì AC<p và BD < p => AC + BD < 2p tổng 2 đường chéo nhỏ hơn chu vi (đpcm)
* giao của AC và BD là O.
trong tam giác OAB có OB + OA > AB , trong tam giác OBC có OB + OC > BC
trong tam giác OADcó OD + OA > AD , trong tam giác ODC có OD + OC > DC
cổng 4 bất đẳng thức cùng chiề này lại ta có:
2.OB + 2.OD + 2.OA + 2.OC > AB + BC + CD + DA
<=> 2 BD + 2 AC > 2p <=> BD + AC > p tổng 2 đường chéo lớn hơn nửa chu vi (đpcm)
Đúng 0
Bình luận (3)
Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn tổng hai cạnh đối.
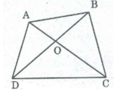
Gọi O là giao điểm của hai đường chéo AC và BD
* Trong ∆ OAB, ta có:
OA + OB > AB (bất đẳng thức tam giác) (1)
* Trong ∆ OCD, ta có:
OC + OD > CD (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2):
OA + OB + OC + OD > AB + CD
⇒ AC + BD > AB + CD
Đúng 0
Bình luận (0)
Chứng minh trong mooth tứ giác thì
a, Tổng độ dài 2 cạnh đối diện nhỏ hơn tổng độ dài hai đường chéo
b, Tổng độ dài hai đường chéo lớn hơn nửa chu vi tứ giác
Chứng minh rằng trong một tứ giác lồi tổng độ dài các cạnh(chu vi) lớn hơn tổng độ dài các đường chéo và nhỏ hơn hai lần tổng độ dài các đương chéo
Chứng minh rằng trong một tứ giác, tổng hai đường chéo lớn hơn tông hai cạnh đối ?
Chứng minh rằng trong một tứ giác thì :
a ) tổng độ dài 2 cạnh đối diện nhỏ hơn tổng độ dài 2 đường chéo
b ) tổng độ dài 2 đường chéo lớn hơn nửa chu vi của tứ giác
Chứng minh rằng trong một tứ giác thì :
a ) tổng độ dài 2 cạnh đối diện nhỏ hơn tổng độ dài 2 đường chéo
b ) tổng độ dài 2 đường chéo lớn hơn nửa chu vi của tứ giác nhưng nhỏ hơn chu vi tứ giác đó
1) chứng minh rằng trong một tứ giác,tổng hai đường chéo lớn hơn tổng hai cạnh đối
2)chứng minh rằng trong một tứ giác,tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy
các bạn giúp mình bài này với
Chứng minh rằng trong tứ giác tổng 2 đường chéo lớn hơn tổng hai cạnh đối
Cho tứ giác có AB =BC , góc A + góc C = 180 độ . Chứng minh rằng BD là tia phân giác của Tam giác ADC
a, Gọi AC giao BD tai O
TAm giác OAB có
OA + OB > AB (1)
Tam giác OCD có
OC + OD > CD (2)
cộng vế với vế của (1) và (2) -=> AC + BD > AB + CD
Đúng 0
Bình luận (0)
Mình cũng đồng ý với ý kiến của bạn
Đúng 0
Bình luận (0)
đúng nhưng bạn thiếu rồi
còn AC+BD>AD+BC nữa
Đúng 0
Bình luận (0)



