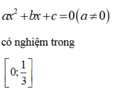Chứng minh rằng phương trình : \(ax^2+bx+c=0\) và \(2a+6b+19c=0\) luôn có một nghiệm dương
NT
Những câu hỏi liên quan
Cho 3 số phân biệt a,b,c ϵ R. Chứng minh rằng phương trình:
\(ax^2+bx+c=0\) luôn có nghiệm trong \(\left[0;\dfrac{1}{3}\right]\) nếu \(2a+6b+19c=0\)
Lời giải:
$f(x)=ax^2+bx+c$ liên tục trên $[0; \frac{1}{3}]$
$f(0)=c$
$f(\frac{1}{3})=\frac{1}{9}a+\frac{1}{3}b+c$
$\Rightarrow 18f(\frac{1}{3})=2a+6b+18c$
$\Rightarrow f(0)+18f(\frac{1}{3})=2a+6b+19c=0$
$\Rightarrow f(0)=-18f(\frac{1}{3})$
$\Rightarrow f(0).f(\frac{1}{3})=-18f(\frac{1}{3})^2\leq 0$
$\Rightarrow$ pt luôn có nghiệm trong $[0; \frac{1}{3}]$ (đpcm)
Đúng 1
Bình luận (0)
Cho phương trình a x 2 + b x + c = 0 a ≠ 0 thỏa mãn 2a + 6b + 19c = 0. Chứng minh phương trình có nghiệm trong 0 ; 1 3
Cho phương trình
a
x
2
+
b
x
+
c
0
thỏa mãn
a
≠
0
và
2
a
+
6
b
+
19
c
0
, với điều kiện đó phương trình có nghiệm
x
0
. Hỏi khẳng định nào sau đây đúng ? A.
x
0
∈...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 thỏa mãn a ≠ 0 và 2 a + 6 b + 19 c = 0 , với điều kiện đó phương trình có nghiệm x 0 . Hỏi khẳng định nào sau đây đúng ?
A. x 0 ∈ 1 ; 2 .
B. x 0 ∈ − 1 3 ; − 1 2 .
C. x 0 ∈ 0 ; 1 3 .
D. x 0 ∈ 0 ; 1 3 .
Đáp án C
Đặt f ( x ) = a x 2 + b x + c là là hàm số đa thức nên liên tục trên .
Ta có: f ( 0 ) = c và
f 1 3 = a 9 + b 3 + c = a + 3 b + 9 c 9 = 2 a + 6 b + 18 c 18 = ( 2 a + 6 b + 19 c ) − c 18 = − c 18
⇒ f ( 0 ) . f 1 3 < 0
KL: Phương trình a x 2 + b x + c = 0 có ít nhất một nghiệm thuộc khoảng 0 ; 1 3
Đúng 0
Bình luận (0)
cho phương trình ax^2+bx+c=0 với các số a,b,c là các số thực nghiệm khác 0 và thỏa mãn điều kiện a+b+2c=0. Chứng minh rằng phương trình trên luôn có nghiệm trên tập số thực
Đặt \(f\left(x\right)=ax^2+bx+c\).
\(f\left(0\right)=c;f\left(1\right)=a+b+c\)
Do \(a+b+2c=0\) nên c và \(a+b+c\) trái dấu. Suy ra f(0)f(1) < 0 nên f(x) = 0 luôn có ít nhất 1 nghiệm tren (0; 1).
Đúng 1
Bình luận (0)
Cho hai phương trình ax2+bx+c=0(a khác 0) và mx2+nx+p=0 (m khác 0).Chứng minh rằng nếu ít nhất một trong hai phương trình trên vô nghiệm thì phương trình sau đây luôn có nghiệm (an-bm)x2 +2(ap-cm)x +bp-cn=0
cho a,b,c là 3 số dương có tổng bằng 12
chứng minh rằng trong 3 phương trình :
x^2 + ax + b =0
x^2+bx+c = 0
x^2 + cx +a =0
có một phương trình vô nghiệm , một phương trình có nghiệm
Các giải của các bài toán này là sử dụng tổng các delta em nhé
Đúng 0
Bình luận (0)
cho x1, x2 là 2 nghiệm dương của phương trình ax^2+bx+c=0
chứng minh phương trình cx^2+ax+b=0 cũng có 2 nghiệm dương x3,x4 và x1+x2+x3+x4>4 ?
a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có
x1 + x2 + x3 + x4 ≥ 4
Đúng 0
Bình luận (0)
cho a,b.c là 3 só thực thỏa mãn 5a+3b+2c = 0.Chứng minh rằng phương trình ax^2 +bx+c = 0 luôn có nghiệm
Cho phương trình: ax2 + bx + c = 0, (a, b, c là các hệ số và a >0).
Chứng minh rằng nếu b > a + c thì phương trình luôn có hai nghiệm phân biệt.
Nếu \(b>a+c\)tương đương với \(b^2>a^2+2ac+c^2\)
Trừ cả 2 vế cho 4ac ta được : \(b^2-4ac>a^2-2ac+c^2=\left(a-c\right)^2\)
Hay \(\Delta>\left(a-c\right)^2\ge0\)
Vậy ta có điều phải chứng mình
b > a + c thì chưa đủ điều kiện chứng minh b^2 > (a + c)^2 mà?
bình phương 2 vế nhé bạn