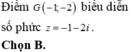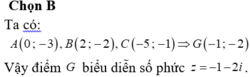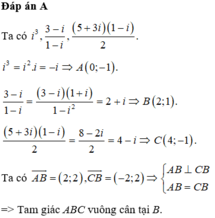Biểu diễn các điểm A(5;0); B(5;-3) trên mặt phẳng tọa độ và xác định điểm đối xứng vs A;B
HA
Những câu hỏi liên quan
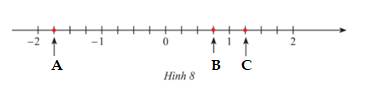
a) Các điểm A,B,C trong Hình 8 biểu diễn số hữu tỉ nào?
b) Biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số.
a) Các điểm A,B,C trong Hình 8 biểu diễn lần lượt các số hữu tỉ: \(\frac{{ - 7}}{4};\,\frac{3}{4};\,\frac{5}{4}.\)
b) Ta có: \(1\frac{1}{5} = \frac{6}{5};\,\,\, - 0,8 = \frac{{ - 8}}{{10}} = \frac{{ - 4}}{5}.\)
Vậy ta biểu diễn các số hữu tỉ \(\frac{{ - 2}}{5};\,1\frac{1}{5};\,\frac{3}{5};\, - 0,8\) trên trục số như sau:

Đúng 0
Bình luận (0)
a) Biểu diễn các số -3; -4; 2; 4 trên trục số. b) Ghi các số nguyên âm nằm giữa các số - 5 và -1 trên trục số c) Trên trục số có điểm nào biểu diễn số nguyên âm nằm giữa các số -5; - 4 không?
a) HS tự biểu diễn. b) Các số nguyên âm gồm có: -4; -3; -2. HS tự biểu diễn. c) Không
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức
z
1
-
3
i
;
z
2
2
-
2
i
;
z
3
5
-
i
. Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là A. z-1-i B. z-1-2i C. z1-2i D. z2-i
Đọc tiếp
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức z 1 = - 3 i ; z 2 = 2 - 2 i ; z 3 = 5 - i . Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là
A. z=-1-i
B. z=-1-2i
C. z=1-2i
D. z=2-i
Từ bài ra ta có A(0;3),B(2;-2),C(-5;-1)
⇒ Trọng tâm G của tam giác ABC có tọa độ
x G = x A + x B + x C 3 = 0 + 2 + ( - 5 ) 3 = - 1 y G = y A + y B + y C 3 = - 3 + ( - 2 ) + ( - 1 ) 3 = - 2
⇒ G(-1;-2)
Điểm G(-1;-2) biểu diễn số phức z=-1-2i.
Chọn đáp án B.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức
z
1
-
3
i
,
z
2
2
-
2
i
,
z
3
-
5
-
i
. Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là
Đọc tiếp
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức z 1 = - 3 i , z 2 = 2 - 2 i , z 3 = - 5 - i . Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là
![]()
![]()
![]()
![]()
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức
z
1
-
3
i
;
z
2
2
-
2
i
;
z
3
-
5
-
i
. Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là A.
z...
Đọc tiếp
Trong mặt phẳng Oxyz, gọi A, B, C lần lượt là các điểm biểu diễn các số phức z 1 = - 3 i ; z 2 = 2 - 2 i ; z 3 = - 5 - i . Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức là
A. z = - 1 - i
B. z = - 1 - 2 i
C. z = 1 - 2 i
D. z = 2 - i
a) Biểu diễn các số –3; –4; 2; 4 trên trục số.
b) Ghi các số nguyên âm nằm giữa các số –5 và –1 trên trục số.
c) Trên trục số có điểm nào biểu diễn số nguyên âm nằm giữa –5 và –4 không?
a) Biểu diễn các số –3; –4; 2; 4 trên trục số.
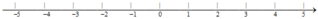
b) Ghi các số nguyên âm nằm giữa các số –5 và –1 trên trục số.
c) Trên trục số không có điểm nào biểu diễn số nguyên âm nằm giữa –5 và –4
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy gọi A,B,C lần lượt là các điểm biểu diễn số phức z1=-3i,z2=2-2i,z3=-5-i. Gọi G là trọng tâm của tam giác ABC. Khi đó điểm G biểu diễn số phức
A. z=-1-i
B.z=-1-2i
C.z=1-2i
D.z=2-i
Biểu diễn các góc lượng giác alpha - frac{{5pi }}{6},;beta frac{pi }{3},;gamma frac{{25pi }}{3},delta frac{{17pi }}{3} trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau? A. beta và gamma B. alpha, beta, gamma C. beta ,gamma ,delta D. alpha và beta ,
Đọc tiếp
Biểu diễn các góc lượng giác \(\alpha = - \frac{{5\pi }}{6},\;\beta = \frac{\pi }{3},\;\gamma = \frac{{25\pi }}{3},\delta = \frac{{17\pi }}{3}\) trên đường tròn lượng giác. Các góc nào có điểm biểu diễn trùng nhau?
A. \(\beta \) và \( \gamma \)
B. \(\alpha, \beta, \gamma \)
C. \(\beta ,\gamma ,\delta \)
D. \(\alpha \) và \(\beta \),
Ta có: \(\frac{{25\pi }}{3} = \frac{\pi }{3} + 4.2\pi .\) Do đó điểm biểu diễn cung lượng giác \(\frac{{25\pi }}{3}\) trùng với điểm biểu diễn cung lượng giác \(\frac{\pi }{3}\).
Vậy ta chọn đáp án A
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức
i
3
,
3
−
i
1
−
i
,
5
+
3
i
1
−...
Đọc tiếp
Trên mặt phẳng tọa độ các điểm A,B,C lần lượt là điểm biểu diễn các số phức i 3 , 3 − i 1 − i , 5 + 3 i 1 − i 2 . Khi đó tam giác ABC.
A. vuông cân tại B
B. đều
C. vuông cân tại A
D. vuông cân tại C