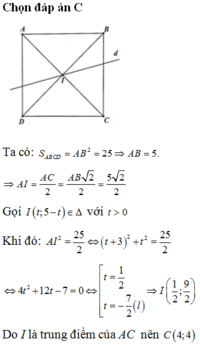Trong mặt phẳng tọa độ Oxy vẽ một hình vuông OABC có A(0; -3); C(3; 0). Vậy tọa độ điểm B là ..............
CH
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy vẽ một hình vuông OABC có A ( 0 ; 3 ) ; C ( 3 ; 0 ) Vậy tọa độ điểm B là ...
Trong mặt phẳng với hệ tọa độ Oxy cho hình bình hành OABC có tọa độ điểm A(3;1), C(-1;2) (tham khảo hình vẽ bên). Số phức nào sau đây có điểm biểu diễn là điểm B? A.
z
1
-
2
+
3
i
B.
z
2
2
+
3
i
C.
z
3
4
-
i
D.
z...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy cho hình bình hành OABC có tọa độ điểm A(3;1), C(-1;2) (tham khảo hình vẽ bên). Số phức nào sau đây có điểm biểu diễn là điểm B?
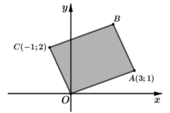
A. z 1 = - 2 + 3 i
B. z 2 = 2 + 3 i
C. z 3 = 4 - i
D. z 4 = - 4 + i
Vì OABC là hình bình hành nên

Suy ra số phức z 2 = 2 + 3 i có điểm biểu diễn là B.
Chọn B.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxy, cho mặt phẳng (P): 2y-z+30 và điểm A (2;0;0). Mặt phẳng (α) đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng 4/3 và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng: A. 8. B. 16 C. 8/3 D. 16/3
Đọc tiếp
Trong không gian với hệ tọa độ Oxy, cho mặt phẳng (P): 2y-z+3=0 và điểm A (2;0;0). Mặt phẳng (α) đi qua A, vuông góc với (P), cách gốc tọa độ O một khoảng bằng 4/3 và cắt các tia Oy, Oz lần lượt tại các điểm B, C khác O. Thể tích khối tứ diện OABC bằng:
A. 8.
B. 16
C. 8/3
D. 16/3
Chọn C
Giả sử B (0;b;0) và C (0;0;c), với b, c > 0.
Khi đó phương trình mặt phẳng (α) là: ![]()
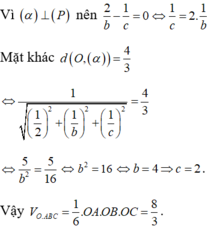
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có A(1; -1) và B(3; 0). Tìm tọa độ điểm D, biết D có tung độ âm.
A.D(0; -1)
B. D( 2; -3)
C. D( 2; -3); D(0; 1)
D. D( -2; -3)
Gọi C= (x, y). Ta có A B → = 2 ; 1 B C → = x − 3 ; y .
Vì ABCD là hình vuông nên ta có A B → ⊥ B C → A B = B C
⇔ 2 x − 3 + 1. y = 0 x − 3 2 + y 2 = 5 ⇔ y = 2 3 − x 5 x − 3 2 = 5 ⇔ y = 2 3 − x x − 3 2 = 1 ⇔ x = 4 y = − 2 hoặc x = 2 y = 2 .
Với C 1 4 ; − 2 ta tính được đỉnh D 1 2 ; − 3 : thỏa mãn.
Với C 2 2 ; 2 ta tính được đỉnh D 2 0 ; 1 : không thỏa mãn.
Chọn B.
Đúng 0
Bình luận (0)
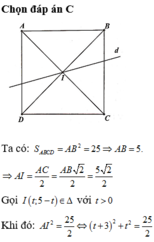
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng
∆
:
x
+
y
-
5
0
và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương.
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng ∆ : x + y - 5 = 0 và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương.
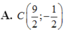
![]()
![]()
![]()
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng
∆
:
x
+
y
-
5
0
và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương A.
C
9
2
;
-
1
2
B. C(1;8) C. C(4;4)...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có đỉnh A(-3;5), tâm I thuộc đường thẳng ∆ : x + y - 5 = 0 và diện tích hình vuông bằng 25. Tìm tọa độ đỉnh C, biết rằng tâm I có hoành độ dương
A. C 9 2 ; - 1 2
B. C(1;8)
C. C(4;4)
D. C(2;2)
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương
Trong không gian với hệ tọa độ Oxy cho mặt phẳng
α
:
2
x
-
y
-
3
z
4
. Gọi A ,B ,C lần lượt là giao điểm của mặt phẳng
α
với các trục tọa độ Ox, Oy, Oz. Thể tích tứ diện OABC bằng: A. 1. B. 2. C.
32
9
D.
16
9
Đọc tiếp
Trong không gian với hệ tọa độ Oxy cho mặt phẳng α : 2 x - y - 3 z = 4 . Gọi A ,B ,C lần lượt là giao điểm của mặt phẳng α với các trục tọa độ Ox, Oy, Oz. Thể tích tứ diện OABC bằng:
A. 1.
B. 2.
C. 32 9
D. 16 9
Trong mặt phẳng tọa độ Oxy cho đường thẳng d 4x+2y+1=0 và điểm A(1;1)
Xác định tọa độ hình chiếu vuông góc của Alên d.
Gọi \(AH\) là hình chiếu của \(A\) trên \(d\)
\(\Rightarrow AH:-2x+4y+c'=0\)
AH đi qua \(A\left(1;1\right)\Rightarrow-2.1+4.1+c'=0\)
\(\Rightarrow c'=-2\)
\(\Rightarrow\) phương trình \(AH\) là : \(-2x+4y-2=0\Rightarrow-x+2y-1=0\)
Tọa độ H là nghiệm của hệ phương trình :
\(\left\{{}\begin{matrix}-x+2y-1=0\\4x+2y+1=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-\dfrac{2}{5}\\y=\dfrac{3}{10}\end{matrix}\right.\)
\(\Rightarrow H\left(-\dfrac{2}{5};\dfrac{3}{10}\right)\)
Đúng 0
Bình luận (0)
Gọi \(\left(d'\right)\) là đường thẳng qua A và vuông góc với (d). Do (d) có VTPT \(\overrightarrow{n_d}=\left(4;2\right)\)
\(\Rightarrow\) \(\left(d'\right)\) có VTPT \(\overrightarrow{n_{d'}}=\left(2;-4\right)\) hay \(\left(d'\right):2x-4y+m=0\) \(\left(m\inℝ\right)\)
Mà \(A\left(1;1\right)\in\left(d'\right)\) nên \(2-4+m=0\Leftrightarrow m=2\). Vậy đường thẳng qua A và vuông góc với \(d\) có pt là \(2x-4y+2=0\) hay \(x-2y+1=0\)
Do đó hình chiếu vuông góc H của A lên d chính là giao điểm của d' và d. Nếu \(H\) có tọa độ \(\left(x_H;y_H\right)\) thì \(x_H;y_H\) thỏa mãn hệ phương trình \(\left\{{}\begin{matrix}x_H-2y_H+1=0\\4x_H+2y_H+1=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_H=-\dfrac{2}{5}\\y_H=\dfrac{3}{10}\end{matrix}\right.\)\(\Rightarrow H\left(-\dfrac{2}{5};\dfrac{3}{10}\right)\).
Vậy hình chiếu của A lên d có tọa độ \(\left(-\dfrac{2}{5};\dfrac{3}{10}\right)\)
Đúng 0
Bình luận (0)