VS
Những câu hỏi liên quan
bài 1: Tính các góc B và D của hình thang ABCD biết rằng góc A60 độ, góc C 130 độBài 2; cmr trong hình thang các tia phân giác của hai góc kề 1 cạnh bên vuông góc vs nhauBài 3; cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng // vs BC, cắt các cạnh AB và AC ở D và Ea, tìm các hình thang trong hình vẽb, cmr hình thang BDEC có 1 cạnh đáy bằng tổng 2 cạnh bên
Đọc tiếp
bài 1: Tính các góc B và D của hình thang ABCD biết rằng góc A=60 độ, góc C= 130 độ
Bài 2; cmr trong hình thang các tia phân giác của hai góc kề 1 cạnh bên vuông góc vs nhau
Bài 3; cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng // vs BC, cắt các cạnh AB và AC ở D và E
a, tìm các hình thang trong hình vẽ
b, cmr hình thang BDEC có 1 cạnh đáy bằng tổng 2 cạnh bên
các bạn giải nhanh nhé mình đang rất gấp
Đúng 0
Bình luận (0)
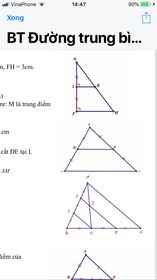
Bài 4: Cho hình vẽ bên. a) Cmr: I là trung điểm AD b) Cmr: FI=1/8 AC
Hình thứ 3 nha
a) Vẽ góc
x
A
y
^
35
0
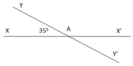
b) Vẽ góc x’Ay’ đối đỉnh với góc xAyc) Viết tên các góc có số đo 350d) Viết tên các góc có số đo 1450
Đọc tiếp
a) Vẽ góc x A y ^ = 35 0
b) Vẽ góc x’Ay’ đối đỉnh với góc xAy
c) Viết tên các góc có số đo 350
d) Viết tên các góc có số đo 1450
a) Vẽ góc x A y ^ = 35 0
b) Vẽ góc x’Ay’ đối đỉnh với góc xAy
c) x A y ^ = x ' A y ' ^ = 35 0
d) x A y ' ^ = x ' A y ^ = 145 0
Đúng 1
Bình luận (0)
Bài 2: Cho hình vẽ bên. Biết rằng GF = 4cm, FH = 3cm, I là trung điểm GF, IK//FH. a) Tính GK. b) Cmr: KGF cân c) Cmr: KFH cân (bằng 2 cách) d) Hạ KM vuông góc với FH. Cmr: M là trung điểm FH(bằng 3 cách) e) Tính độ dài IM.

a) Ta có: \(GI=IF=\dfrac{GF}{2}\) ( do I là trung điểm GF)
\(\Rightarrow GI=GF=\dfrac{4}{2}=2\left(cm\right)\)
Xét ΔABC có:
I là trung điểm của GF(gt)
IK//FH(gt)
=> K là trung điểm của GH
=> IK là đường trung bình của tam giác ABC
=> \(IK=\dfrac{1}{2}FH=\dfrac{1}{2}.3=\dfrac{3}{2}\)(cm)
Xét tam giác GIK vuông tại I có:
\(GK^2=GI^2+IK^2\)( định lý Pytago)
\(\Rightarrow GK=\sqrt{GI^2+IK^2}=\sqrt{2^2+\left(\dfrac{3}{2}\right)^2}=\dfrac{5}{2}\left(cm\right)\)
b) Xét tam giác KGF có:
\(KI\perp GF\)( KI //FH, FH⊥GF=> KI⊥GF)
KI là đường trung tuyến( I là trung điểm của GF)
=> Tam giác KGF cân tại K
c) Cách 1:
Xét tam giác GCH vuông tại C có
FK là đường trung tuyến ứng với cạnh huyền GH( K là trung điểm của GH)
=> \(FK=\dfrac{1}{2}GH=KH\) \(\Rightarrow\Delta FKH\) cân tại K
Cách 2:
Xét tam giác GFH có:
IK là đường trung bình
=> IK//FH \(\Rightarrow\left\{{}\begin{matrix}\widehat{IKF}=\widehat{KFH}\\\widehat{GKI}=\widehat{KHF}\end{matrix}\right.\)
Mà \(\widehat{GKI}=\widehat{IKF}\) ( do tam giác GKF cân tại K nên KI là tia phân giác \(\widehat{GKF}\))
\(\Rightarrow\widehat{KFH}=\widehat{KHF}\Rightarrow\Delta KFH\) cân tại K
Đúng 0
Bình luận (0)
d) Cách 1:
Xét tam giác KFH cân tại K có:
KM là đường cao ( KM⊥FH)
=>KM là đường trung tuyến => M là trung điểm của FH
Cách 2:
Xét tứ giác IKMF có:
\(\widehat{KIF}=\widehat{IFM}=\widehat{FMK}=90^0\) => Tứ giác IKMF là hình chữ nhật
=> IK =FM mà \(FM=\dfrac{1}{2}FH\Rightarrow IK=\dfrac{1}{2}FH\Rightarrow M\) là trung điểm của FH
Cách 3:
Xét tam giác GFH có:
K là trung điểm của GH(IK là đường trung bình)
KM//GF( cùng vuông góc với FH)
=> M là trung điểm của FH
e) Xét tam giác GCH vuông tại C có:
\(GH^2=GC^2+CH^2\Rightarrow GH=\sqrt{GC^2+CH^2}=\sqrt{4^2+3^2}=5\left(cm\right)\)
Ta có: Tứ giác IKMF là hình chữ nhật
\(\Rightarrow IM=FK=\dfrac{1}{2}GH=\dfrac{1}{2}.5=\dfrac{5}{2}\left(cm\right)\)
Đúng 1
Bình luận (0)
Bài 3: Cho hình vẽ bên. Biết DE = 4 cm, D là trung điểm AB, E là trung điểm AC a) Tính BC. b) Gọi M là trung điểm BC. AM cắt DE tại I. Cmr: I là trung điểm DE. c) AM cắt BE tại G. Cmr: IG=1/6 AM
Hình thứ 2 nha
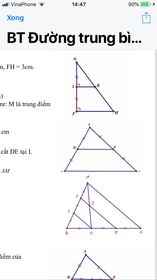
cho tam giác ABC các tia phân giác của góc B và góc C cắt nhau tại I qua I kẻ đg thẳng song song BC CẮT các cạnh AB và AC ở D và E a) tìm CÁC hình thang trong hình vẽ
b) cmr hình thang BDEC có 1 cạnh đáy = tổng 2 cạnh bên
trên một đường thanh lấy 4 điểm A B C D Sao cho C nằm giữa A và B ;B nằm giữa C và D Biết AB=5cm AD =8cm BC=2cm Hãy vẽ hình và CMR AC=BD; CD=AB
Giải hộ mình với
cho tam giác ABC vuông tại A có góc C dfrac{1}{2} góc B. Kẻ AH⊥ BC tại H. Trên tia HC lấy D sao cho HD HB. Từ C kẻ CE⊥AD
a)Δ ABD là △ gì ? tại sao ?
b)CMR : AD CD ; DE DH ; HE // AC
c)So sánh 4HE2 và BC2- AD2
d)Gọi K là giao điểm của AH và CE lấy điểm I bất kì trên HE (I≠H,E)
CMR: dfrac{3}{2}AC IA + IC + IK
Đọc tiếp
cho tam giác ABC vuông tại A có góc C = \(\dfrac{1}{2}\) góc B. Kẻ AH⊥ BC tại H. Trên tia HC lấy D sao cho HD = HB. Từ C kẻ CE⊥AD
a)Δ ABD là △ gì ? tại sao ?
b)CMR : AD = CD ; DE = DH ; HE // AC
c)So sánh 4HE2 và BC2- AD2
d)Gọi K là giao điểm của AH và CE lấy điểm I bất kì trên HE (I≠H,E)
CMR: \(\dfrac{3}{2}\)AC < IA + IC + IK
chu vi là 78 cm
chu vi là 270 cm2 nha
Đúng 0
Bình luận (0)
chu vi là 78 cm
chu vi là 270 cm2 nha
Đúng 1
Bình luận (0)
Cho hình vẽ bên cho biết
a // b
và
A
^
1
−
B
^
2
70
0
. Hãy tính
A
^
3
và
B
^
4
Đọc tiếp
Cho hình vẽ bên cho biết a // b và A ^ 1 − B ^ 2 = 70 0 . Hãy tính A ^ 3 và B ^ 4
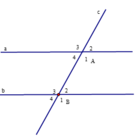
+) Vì a // b nên A ^ 1 + B ^ 2 = 180 ∘ (cặp góc trong cùng phía)
Mặt khác A ^ 1 − B ^ 2 = 70 0
⇒ A ^ 1 = 180 ∘ + 70 ∘ : 2 = 125 ∘ và B ^ 2 = 180 ∘ − 125 ∘ = 55 ∘
+) Ta có A ^ 3 = A ^ 1 (hai góc đối đỉnh) mà A ^ 1 = 125 ∘
⇒ A ^ 3 = 125 ∘
Ta có B ^ 2 = B ^ 4 (hai góc đối đỉnh) mà B ^ 2 = 55 ∘
⇒ B ^ 4 = 55 ∘
Đúng 0
Bình luận (0)



