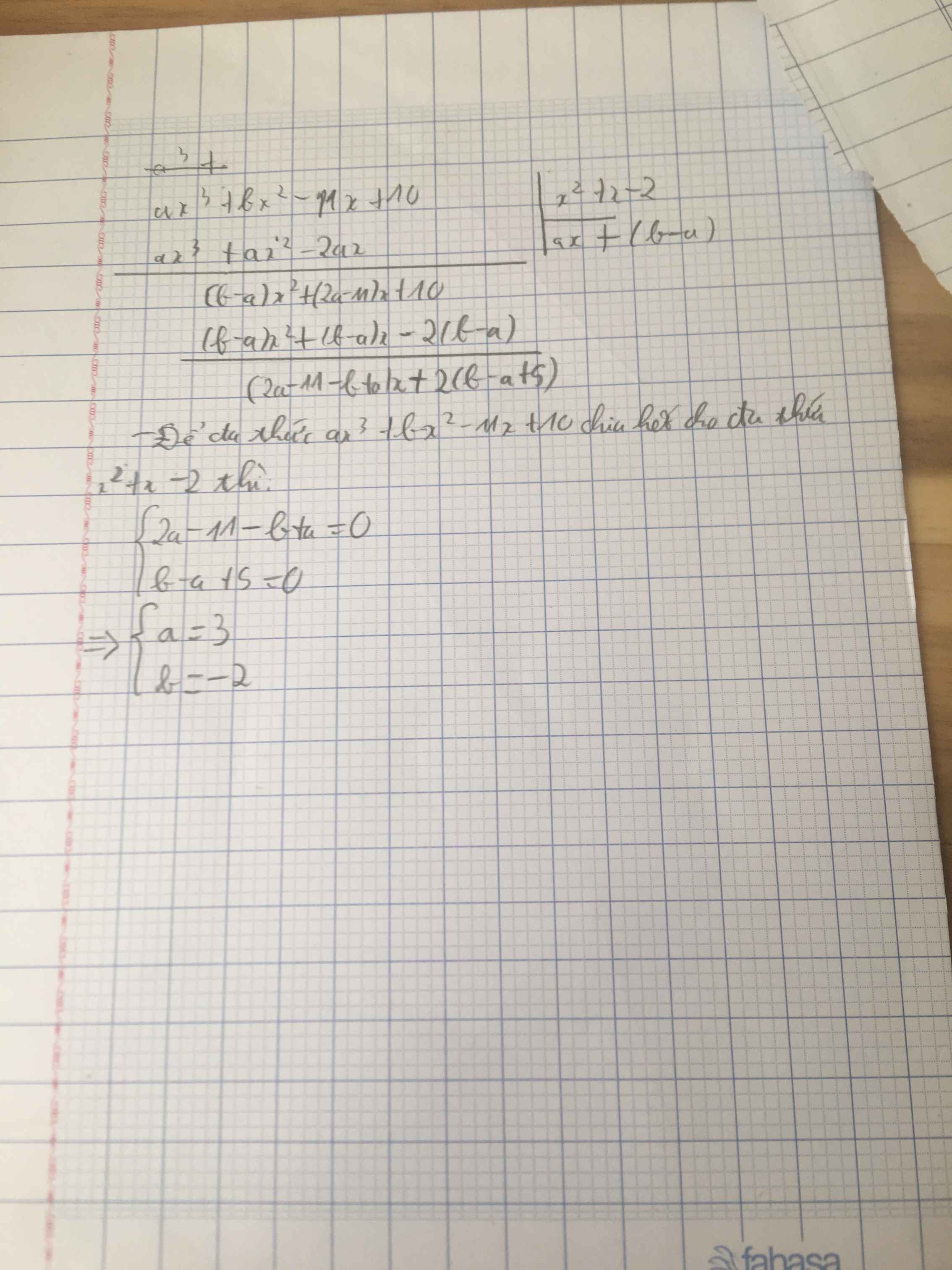xác định a,b để P(x)= ax^4+bx^3+1 chia hết cho đa thức Q(x)=(x-1)^2
LC
Những câu hỏi liên quan
Xác định các hằng số a và b sao cho
a) x^4 + ax + b chia hết cho x^2 - 4
b) x^4 + ax^ + bx - 1 chia hết cho x^2 - 1
c) x^3 + ax + b chia hết cho x^2 + 2x - 2
(Chia đa thức cho đa thức)

Chỉ ý kiến của mk thôi
chưa chắc đúng
Tham khảo nhé
Đúng 0
Bình luận (0)
tìm và xác định số hiệu tỷ a,b sao cho : 3x^3+ax^2+bx+9 chia hết cho đa thức x^2-9
B) x^4+ax^33+bx-1 chia hết cho x^2-1
xác định a và b sao cho đa thức ax^4 + bx^3 + 1 chia hết cho (x-1)^2
Cho P(x) = ax^4 + bx^3 +1 và Q (x) = (x−1)^2 . Xác định a, b để: P(x) chia hết cho Q(x)
Xác định các số a và b để đa thức ax^3+bx^2-11x+10 chia hết cho đa thức x^2+x-2
Lời giải:
Đặt $f(x)=ax^3+bx^2-11x+10$
$x^2+x-2=(x-1)(x+2)$
Do đó để $f(x)\vdots x^2+x-2$ thì $f(x)\vdots x-1$ và $f(x)\vdots x+2$
$\Leftrightarrow f(1)=f(-2)=0$ (theo định lý Bê-du về phép chia đa thức)
$\Leftrightarrow a+b-1=-8a+4b+32=0$
$\Leftrightarrow a=3; b=-2$
Đúng 1
Bình luận (0)
Xác định các hệ số a,b,c để đa thức:
\(f\left(x\right)=x^5-2x^4-6x^3+ax^2+bx+c\) chia hết cho đa thức \(g\left(x\right)=\left(x^2-1\right)\left(x-3\right)\)
Để \(f\left(x\right)⋮g\left(x\right)\)thì \(f\left(x\right)=g\left(x\right)\cdot q\)( với q là hằng số )
Khi đó ta có pt :
\(x^5-2x^4-6x^3+ax^2+bx+c=\left(x^2-1\right)\left(x-3\right)\cdot q\)
\(\Leftrightarrow x^5-2x^4-6x^3+ax^2+bx+c=\left(x-1\right)\left(x+1\right)\left(x-3\right)\cdot q\)
Vì pt trên đúng với mọi x nên :
+) đặt \(x=1\)
\(pt\Leftrightarrow1^5-2\cdot1^4-6\cdot1^3+a\cdot1^2+b\cdot1+c=\left(1-1\right)\left(1+1\right)\left(1-3\right)\cdot q\)
\(\Leftrightarrow-7+a+b+c=0\)
\(\Leftrightarrow a+b+c=7\)(1)
Chứng minh tương tự, lần lượt đặt \(x=-1\)và \(x=3\)ta có các pt :
\(\hept{\begin{cases}3+a-b+c=0\\-81+9a+3b+c=0\end{cases}\Leftrightarrow\hept{\begin{cases}a-b+c=-3\\9a+3b+c=81\end{cases}}}\)(2)
Từ (1) và (2) ta có hệ pt 3 ẩn :
\(\hept{\begin{cases}a+b+c=7\\a-b+c=-3\\9a+3b+c=81\end{cases}}\)
Giải hệ ta được \(\hept{\begin{cases}a=8\\b=5\\c=-6\end{cases}}\)
Vậy....
Đúng 0
Bình luận (0)
xác định hệ số a,b sao cho đa thức x4+ax3+bx+b chia hết cho đa thức x2-1
Đặt f(x) = x^4 + ax^3 + bx +b
xét f(-1)=0 và f(1) =0(vì f(x) chia hết cho a khi f(a) =0)
f(-1) = 1 - a -b + b = 1-a =0
+
f(1) = 1+a+b+b = 1+a+2b = 0
-------------------------------------------
=> 2+2b = 0
=> b= -1
=> 1+a-2 = 0
=> a=1
Đúng 0
Bình luận (0)
Cho đa thức P(x) = 6x4 - 7x3-12x2 +ax+2 và Q(x) = x2 + bx - 2
Xác định a;b(dưới dạng số hoặc phân số) để đa thức P(x) chia hết cho Q(x)
làm gấp nhaBaì 1 .cho đa thức P(x)ax^2+bx+c biết 2a+3b+6c0a) Tính a,b,c thep P(0);P(1/2);P(1)b) CMR P(0);P(1/2);P(1) không thể cùng âm hoặc cùng dươngc) CMR đa thức P(x) có 1 nghiệm dương bé hơn 1Bài 2. Cho P(x)ax^4+bx^3+1 Q(x)(x-1)^2Xác định a,b sao cho P(x) chia hết cho Q(x)Bài 3.Cho P(x)6x^4-7x^3+ax^2+3x+2 Q(x)x^2-x+bXác định a,b sao cho P(x) chia hết cho Q(x)
Đọc tiếp
làm gấp nha
Baì 1 .cho đa thức P(x)=ax^2+bx+c biết 2a+3b+6c=0
a) Tính a,b,c thep P(0);P(1/2);P(1)
b) CMR P(0);P(1/2);P(1) không thể cùng âm hoặc cùng dương
c) CMR đa thức P(x) có 1 nghiệm dương bé hơn 1
Bài 2. Cho P(x)=ax^4+bx^3+1
Q(x)=(x-1)^2
Xác định a,b sao cho P(x) chia hết cho Q(x)
Bài 3.Cho P(x)=6x^4-7x^3+ax^2+3x+2
Q(x)=x^2-x+b
Xác định a,b sao cho P(x) chia hết cho Q(x)