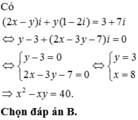số các giá trị của x thỏa mãn (x^2-2x)I3x-7I=0
HH
Những câu hỏi liên quan
Giúp mình với
Số các giá trị thỏa mãn của x
(x^2 -2x) I3x-7I = 0
Gấp lắm bạn ơi ! =)
(x2-2x) |3x-7| =0
x2-2x= 0|3x-7|
x2-2x= 0
x2=0+2x
x2=2x
=> x\(\in\){ 0,1}
Sai thì thôi, chết thì chôn nha bạn. đừng trách mik, mik dốt toán lắm
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
CÁc câu hỏi này nhé, mình gắp lắm:
1) Số cặp (x:y) thỏa mãn
x(x+y)=-45
y(x+y)=5
2)Giá trị của x biết
(1/2)^-x+4=(1/4)^3/2-4
3) Số các giá trị của giá trị x thỏa mãn :
( x^2 - 2x) I 3x - 7I =0
4) Giá trị lớn nhất cảu
A= x+ 1/2 - I x - 2/3I
Hai chữ số tận cùng của 51^51 2. Trung bình cộng của các giá trị của x thỏa mãn: (x - 2)^8 (x - 2)^6 3. Số x âm thỏa mãn: 5^(x - 2).(x + 3) 1 4. Số nguyên tố x thỏa mãn: (x - 7)^x+1 - (x - 7)^x+11 0 5. Tổng 3 số x,y,y biết: 2x y; 3y 2z và 4x - 3y + 2z 36 6. Tập hợp các số hữu tỉ x thỏa mãn đẳng thức: x^2 - 25.x^4 0 7. Giá trị của x trong tỉ lệ thức: 3x+2/5x+7 3x-1/5x+1 8. Giá trị của x thỏa mãn: (3x - 2)^5 -243 9. Tổng của 2 số x,y thỏa mãn: !x-2007! !y-2008! hoặc 0 10. số hữu tỉ dư...
Đọc tiếp
Hai chữ số tận cùng của 51^51
2. Trung bình cộng của các giá trị của x thỏa mãn: (x - 2)^8 = (x - 2)^6
3. Số x âm thỏa mãn: 5^(x - 2).(x + 3) = 1
4. Số nguyên tố x thỏa mãn: (x - 7)^x+1 - (x - 7)^x+11 = 0
5. Tổng 3 số x,y,y biết: 2x = y; 3y = 2z và 4x - 3y + 2z = 36
6. Tập hợp các số hữu tỉ x thỏa mãn đẳng thức: x^2 - 25.x^4 = 0
7. Giá trị của x trong tỉ lệ thức: 3x+2/5x+7 = 3x-1/5x+1
8. Giá trị của x thỏa mãn: (3x - 2)^5 = -243
9. Tổng của 2 số x,y thỏa mãn: !x-2007! = !y-2008! < hoặc = 0
10. số hữu tỉ dương và âm x thỏa mãn: (2x - 3)^2 = 16
11. Tập hợp các giá trị của x thỏa mãn đẳng thức: x^6 = 9.x^4
12. Số hữu tỉ x thỏa mãn: |x|. |x^2+3/4| = X
có khùng hk vậy hùng tự đăng tự giải ls
Đúng 0
Bình luận (0)
1) Quy luật cứ mũ chẵn 2 số tận cùng là 01 còn mũ lẻ thì 2 số tận cùng là 51
Vậy 2 số tận cùng của 51^51 là 51
2)pt<=> x-2=0 hoặc (x-2)^2=1 <=> x=2 hoặc x=1 hoặc x=3
Vậy trung bìng cộng là 2
4)Pt<=> (x-7)^(x+1)=0 hoặc 1-(x-7)^10=0=> x=7 hoặc x=8 hoặc x=6
Do x là số nguyên tố => x=7 TM
5)3y=2z=> 2z-3y=0
4x-3y+2z=36=> 4x=36=> x=9
=> y=2.9=18=> z=3.18/2=27
=> x+y+z=9+18+27=54
6)pt<=> x^2=0 hoặc x^2=25 <=> x=0 hoặc x=-5 hoặc x=5
7)pt<=> (3x+2)(5x+1)=(3x-1)(5x+7)
Nhân ra kết quả cuối cùng là x=3
8)ta có (3x-2)^5=-243=-3^5
=> 3x-2=-3 => x=-1/3
9)Câu này chưa rõ ý bạn muốn hỏi!
10)2x-3=4 hoặc 2x-3=-4
<=> x=7/2 hoặc x=-1/2
11)x^4=0 hoặc x^2=9
=> x=0 hoặc x=-3 hoặc x=3
Đúng 0
Bình luận (0)
anh đang chia sẻ kiến thức đóa à
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
số các giá trị của x thỏa mãn : (x2-2x).l3x-7l=0
Cho số thực x, y thỏa mãn
2
x
-
y
i
+
i
1
-
2
i
3
+
7
i
với i là đơn vị ảo. Giá trị của
x
2
-
x
y
bằng A. 30 B. 40 C. 10 D. 20
Đọc tiếp
Cho số thực x, y thỏa mãn 2 x - y i + i 1 - 2 i = 3 + 7 i với i là đơn vị ảo. Giá trị của x 2 - x y bằng
A. 30
B. 40
C. 10
D. 20
Số các giá trị của x thỏa mãn : ( x2 - 2x ) | 3x - 7 | = 0
Th1:x2-2x=0(*)
<=>x*x-2x=0
=>x(x-2)=0
trường hợp này lại chia ra 2 Th nhỏ
TH1:x=0;
TH2:x-2=0
=>x=2
Th2:|3x-7|=0
=>3x-7=±0
=>3x=7
=>x=\(\frac{7}{3}\)
ủng hộ nhá ^^
Đúng 0
Bình luận (0)
Cho số thực x, y thỏa mãn (2x-y)i+y(1-2i)=3+7i với i là đơn vị ảo. Giá trị của x 2 - x y bằng
A. 30
B. 40
C. 10
D. 20
Tìm các số nguyên x,y thỏa mãn:6xy+4x-9y-7=0
Tìm giá trị nhỏ nhất của A=x^3+y^3+xy với x,y dương thỏa mãn x+y=1
Tìm các số nguyên x,y thỏa mãn 2x^2+1/x^2+y^2/4=4 sao cho xy đạt giá trị lớn nhất
HELP !
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
Đúng 0
Bình luận (0)
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
tập hợp các giá trị của x thỏa mãn : x4-2x3+10x2-20x = 0
tập hợp các giá trị của x thỏa mãn khác 0: x+x2-x3-x4
x4-2x3+10x2-20x=0 =>x3(x-2)+10x(x-2)=0 =>(x-2)(x3+10x)=0 =>x(x-2)(x2+10)=0
=>x=0 hoặc x=2 hoặc x= - căn 10
Đúng 0
Bình luận (0)