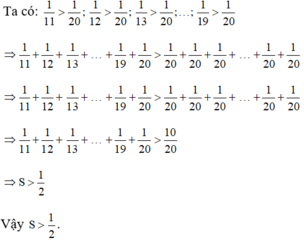Cho A= 1+112+113+114+...+119 Chứng minh A chia hết cho 5
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
TP
Những câu hỏi liên quan
Chứng minh rằng:
a
)
A
1
12
+
1
13
+
1
14
+
...
+
1
22...
Đọc tiếp
Chứng minh rằng:
a ) A = 1 12 + 1 13 + 1 14 + ... + 1 22 > 1 2 b ) B = 1 6 + 1 7 + 1 8 + ... + 1 18 + 1 19 < 2 c ) C = 1 10 + 1 11 + 1 12 + ... + 1 99 + 1 100 > 1
a) A = 1 12 + 1 13 + 1 14 + ... + 1 22 > 1 22 + 1 22 + ... 1 22 ⏟ 11 s = 11 22 = 1 2 .
b) B = 1 6 + ... 1 9 + 1 10 + ... + 1 19 < 1 4 + ... + 1 4 ⏟ 4 s o + 1 10 + ... + 1 10 ⏟ 10 s o = 2
c) C = 1 10 + 1 11 + ... + 1 100 > 1 10 + 1 100 = ... + 1 100 ⏟ 90 s o = 1 10 + 90 100 = 1
Đúng 0
Bình luận (0)
Chứng minh rằng: A = 1 12 + 1 13 + 1 14 + ... + 1 22 > 1 2
A = 1 12 + 1 13 + 1 14 + ... + 1 22 > 1 22 + 1 22 + ... 1 22 ⏟ 11 s = 11 22 = 1 2 .
Đúng 0
Bình luận (0)
Chứng minh rằng: A = 1 12 + 1 13 + 1 14 + ... + 1 22 > 1 2
A = 1 12 + 1 13 + 1 14 + ... + 1 22 > 1 2 ⇔ 1 12 + 1 13 + 1 14 + ... + 1 22 > 11 22 ⇔ 1 12 − 1 22 + 1 13 − 1 22 + 1 14 − 1 22 + ... + 1 22 − 1 22 > 0
Vì 1 12 > 0 , 1 13 > 0 , ... , 1 21 > 1 22 nên 1 12 − 1 22 > 0 , 1 13 − 1 22 > 0 , ... , 1 21 − 1 22 > 0 , 1 22 − 1 22 = 0
Suy ra A > 1 2
Đúng 0
Bình luận (0)
Chứng minh rằng:
a
)
A
1
11
+
1
12
+
1
13
+
...
+
1
20...
Đọc tiếp
Chứng minh rằng:
a ) A = 1 11 + 1 12 + 1 13 + ... + 1 20 > 1 2 b ) B = 1 5 + 1 6 + 1 7 + ... + 1 16 + 1 17 < 2 c ) C = 1 10 + 1 11 + 1 12 + ... + 1 18 + 1 19 < 1
a) A > 1 20 + 1 20 + ... + 1 20 ⏟ 10 s o = 10 20 = 1 2 .
b) B = 1 5 + ... 1 9 + 1 10 + ... + 1 17 < 1 5 + ... + 1 5 ⏟ 5s o + 1 8 + ... + 1 8 ⏟ 8s o = 2
c) C = 1 10 + 1 11 + 1 12 ... + 1 18 + 1 19 < 1 10 + 1 10 + ... 1 10 ⏟ 9 s o = 1
Đúng 0
Bình luận (0)
Cho:
S
1
11
+
1
12
+
1
13
+
1
14
+
1
15
+
1
16
+
1
17
+
1
18
+
1
19
+
1
2...
Đọc tiếp
Cho:
S = 1 11 + 1 12 + 1 13 + 1 14 + 1 15 + 1 16 + 1 17 + 1 18 + 1 19 + 1 20
Hãy so sánh S và 1 2
Cho A=50/111+50/112+50/113+50/114.Chứng tỏ 1<A<2
Ta có :
\(A=\dfrac{50}{111}+\dfrac{50}{112}+\dfrac{50}{113}+\dfrac{50}{114}\)
Ta thấy :
\(\dfrac{50}{111}>\dfrac{50}{200}\)
\(\dfrac{50}{112}>\dfrac{50}{200}\)
\(\dfrac{50}{113}>\dfrac{50}{200}\)
\(\dfrac{50}{114}>\dfrac{50}{200}\)
\(\Rightarrow A>\dfrac{50}{200}+\dfrac{50}{200}+\dfrac{50}{200}+\dfrac{50}{200}\)
\(\Rightarrow A>\dfrac{50}{200}.4=1\) \(\left(1\right)\)
Mặt khác :
\(\dfrac{50}{111}< \dfrac{50}{100}\)
\(\dfrac{50}{112}< \dfrac{50}{100}\)
\(\dfrac{50}{113}< \dfrac{50}{100}\)
\(\dfrac{50}{114}< \dfrac{50}{100}\)
\(\Rightarrow A< \dfrac{50}{100}+\dfrac{50}{100}+\dfrac{50}{100}+\dfrac{50}{100}\)
\(\Rightarrow A< \dfrac{50}{100}.4=2\) \(\left(2\right)\)
Từ \(\left(1\right)+\left(2\right)\Rightarrow1< A< 2\rightarrowđpcm\)
Đúng 0
Bình luận (0)
119 + 118 + 117 + 116 + 115 + 114 + 113 + 112 + 111 + 100 = giúp mik nha
= 1135 nha ban chuc ban hoc gioi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tinh A=1+2-3-4+5+6-7-8+...-111-112+113+114
giup minh nhe
áp dụng công thức \(\frac{n\left(n-1\right)}{2}\)
<=>\(\frac{114\cdot\left(114-1\right)}{2}\)
<=> A =6441
Đúng 0
Bình luận (0)
A=1+2-3-4+5+6-7-8+...-111-112+113+114
A=1+(2-3-4+5)+(6-7-8+9)+...+(110-111-112+113)+114
A=1+ 0 +0 +.........+0+114
A=115
Đúng 0
Bình luận (0)
A = 1 + 2 - 3 - 4 + 5 + 6 - 7 - 8 + ... - 111 - 112 + 113 + 114 ( có 114 số, 114 chia 4 dư 2)
A = 1 + ( 2 - 3 - 4 + 5) + ( 6 - 7 - 8 + 9) + ... + ( 110 - 111 - 112 + 113) + 114
A = 1 + 0 + 0 + ... + 0 + 114
A = 115 + 0
A = 115
Đúng 0
Bình luận (0)
cho A=119+118+...+11+1 chứng minh A chia hết cho 5
c
òi cậu viết sai hết đề thế này mk bt cậu nên làm hộ vậy!
Đúng 0
Bình luận (0)
A = 11^9 + 11^8 + ... + 11 + 1
=> 11A = 11^10 + 11^9 +..........+ 11^2 + 11
11A - A = (11^10 + 11^9 +..........+ 11^2 + 11 ) - (11^9 + 11^8 + ... + 11 + 1)
10A = 11^10 - 1
A = (11^10 - 1 ) : 10
vì 11^10 có tận cùng = 1 => (11^10 - 1) có tận cùng = 0 =>(11^10 - 1 ) : 10 có tận cùng là 0 .
. Vậy A chia hết cho 5
Đúng 0
Bình luận (0)
Chứng minh rằng : A = 119 + 118 +...................... + 11 + 1 chia hết cho 5
sửa đề : CMR \(A=1^{19}+1^{18}+...+1^1+1\)
A = 1 + 1 + ... + 1 + 1 ( 20 số hạng )
A = 20 chia hết cho 5 => A chia hết cho 5 ( đpcm )