xét tính đúng sai mệnh đề sau
Nếu 122 + 52 = 132 thì 0 ≥ 0
Xét hai mệnh đề sau:
(1) Nếu ABC là tam giác đều thì nó là tam giác cân
(2) Nếu 2a – 4 > 0 thì a > 2
a) Xét tính đúng sai của mỗi mệnh đề trên.
b) Mỗi mệnh đề trên đều có dạng “Nếu P thì Q”. Chỉ ra P và Q ứng với mỗi mệnh đề đó.
a)
(1) “Nếu ABC là tam giác đều thì nó là tam giác cân” là mệnh đề đúng.
(2) “Nếu 2a – 4 >0 thì a > 2” là mệnh đề đúng.
b) Trong mệnh đề (1) “Nếu ABC là tam giác đều thì nó là tam giác cân”
P: “ABC là tam giác đều”
Q: “ABC là tam giác cân”
Trong mệnh đề (2) “Nếu 2a – 4 > 0 thì a > 2”
P: “2a – 4 > 0”
Q: “a > 2”
Chú ý
Từ “nó” trong mênh đề (1) được hiểu là “ABC”. Do đó khi chỉ ra mệnh đề Q, ta dùng “ABC” thay cho “nó” để mệnh đề được rõ nghĩa.
Xét hai mệnh đề dạng \(P \Rightarrow Q\) sau:
“Nếu ABC là tam giác đều thì nó có hai góc bằng \({60^o}\)”;
“Nếu \(a = 2\) thì \({a^2} - 4 = 0\)”.
a) Chỉ ra P, Q và xét tính đúng sai của mỗi mệnh đề trên.
b) Với mỗi mệnh đề đã cho, phát biểu mệnh đề \(Q \Rightarrow P\) và xét tính đúng sai của nó.
a)
+) Mệnh đề R: “Nếu ABC là tam giác đều thì nó có hai góc bằng \({60^o}\)” có dạng \(P \Rightarrow Q\), với
P: “ABC là tam giác đều” và Q: “Tam giác ABC có hai góc bằng \({60^o}\)”
Ta thấy khi P đúng thì Q cũng đúng. Do đó \(P \Rightarrow Q\) đúng hay R đúng.
+) Mệnh đề T: “Nếu \(a = 2\) thì \({a^2} - 4 = 0\)” có dạng \(P \Rightarrow Q\), với:
P: “\(a = 2\)” và Q: “\({a^2} - 4 = 0\)”.
Ta thấy khi P đúng thì Q cũng đúng. Do đó \(P \Rightarrow Q\) đúng hay T đúng.
b) Mệnh đề \(Q \Rightarrow P\) của hai mệnh đề trên là:
“Nếu ABC có hai góc bằng \({60^o}\) thì nó là tam giác đều”, đúng.
“Nếu \({a^2} - 4 = 0\) thì \(a = 2\)” sai (vì thiếu nghiệm \(a = - 2\)).
Xét tính đúng sai của mỗi mệnh đề sau và phát biểu mệnh đề phủ định của nó: |-125| ≤ 0
Mệnh đề ‘’|–125| ≤ 0’’ sai vì |–125| = 125 > 0
Mệnh đề phủ định: "|–125| > 0"
Xét tính đúng, sai của các mệnh đề sau rồi lập mệnh đề phủ định của chúng.
𝐴: "∀𝑥 ∈ 𝑅, 𝑥 2 > 0".
Lời giải:
Mệnh đề sai, do với $x=0\in\mathbb{R}$ thì $x^2=0$
Mệnh đề phủ định:
$\overline{A}: \exists x\in\mathbb{R}, x^2\leq 0$
Xét tính đúng sai của mỗi mệnh đề sau và phát biểu phủ định của nó: 3 + 12 2 là một số hữu tỉ
Mệnh đề đúng, vì 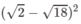 là một số vô tỉ”, mệnh đề này sai.
là một số vô tỉ”, mệnh đề này sai.
Xét tính đúng - sai của các mệnh đề sau. Nếu mệnh đề sai hãy sửa lại cho đúng:
giúp mình với
Phát biểu thành lời các mệnh đề sau và xét tính đúng sai của chúng. ∀ x ∈ R : x 2 ≤ 0
Bình phương của mọi số thực đều nhỏ hơn hoặc bằng 0 (mệnh đề sai).
Phát biểu thành lời các mệnh đề sau và xét tính đúng sai của chúng. ∃ x ∈ R : x 2 ≤ 0
Có một số thực mà bình phương của nó nhỏ hơn hoặc bằng 0 (mệnh đề đúng).
tìm mệnh đề phủ định và xét tính đúng sai của mệnh đề
∀ϵR: x2 -3x+5 ≠0
Lời giải:
Mệnh đề gốc: Đúng, do $x^2-3x+5=(x-1,5)^2+2,75\geq 2,75>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow x^2-3x+5\neq 0, \forall x\in\mathbb{R}$
Mệnh đề phủ định: $\exists x\in\mathbb{R}, x^2-3x+5=0$
Cho hàm số có f đạo hàm trên khoảng I. Xét các mệnh đề sau:
(I). Nếu , thì hàm f '(x) < 0 "x ∈ I số nghịch biến trên I
(II). Nếu , f '(x) ≤ 0 "x ∈ I (dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I ) thì hàm số nghịch biến trên I
(III). Nếu , thì hàm f '( x) ≤ 0 "x ∈ I số nghịch biến trên khoảng I
(IV). Nếu , f '(x) ≤ 0 "x ∈ I và f '(x) = 0 tại vô số điểm trên thì hàm I số không f thể nghịch biến trên khoảng I
Trong các mệnh đề trên. Mệnh đề nào đúng, mệnh đề nào sai?
A. I, II và IV đúng, còn III sai.
B. I, II, III và IV đúng.
C. I và II đúng, còn III và IV sai.
D. I, II và III đúng, còn IV sai.
Đáp án là C
Câu III sai vì thiếu dấu bằng chỉ xảy ra tại một số hữu hạn điểm trên I
Câu IV sai vì có thể vô số điểm trên I xuất hiện rời rạc thì vẫn có thể nghịch biến trên khoảng I