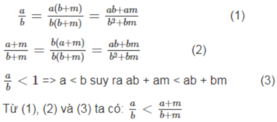Cho a,m,b là số nguyên, m>0 và a/m < b/m. Chứng tỏ rằng: a/m < a+b / 2×m < b/m
DA
Những câu hỏi liên quan
cho phân số a/b ( a,b thuộc N , b khác 0 )
1. Nếu a/b < 1 và m thuộc N , m khác 0 . Chứng tỏ rằng :
a/b < a+m/b+m
2. Nếu a/b > 1 và m thuộc N , m khác 0 . Chứng tỏ rằng :
a/b > a+m/b+m
1. Do \(\frac{a}{b}< 1\Leftrightarrow\)a<b \(\Leftrightarrow\)a+n<b+n
Ta có: \(\frac{a}{b}\)= 1 - \(\frac{a-b}{b}\)
\(\frac{a+n}{b+n}\)= 1- \(\frac{a-b}{b+n}\)
Do \(\frac{a-b}{b}\)>\(\frac{a-b}{b+n}\)=> \(\frac{a}{b}\)<\(\frac{a+n}{b+n}\)
2.Tương tự
Đúng 0
Bình luận (0)
cho M =a/a+b + b/b+c + c/c+a với a,b,c >0
chứng tỏ rằng M không phải là số nguyên
M = a / a+b = b / b+c = c / c+a = a + b + c / (a+b) + (b+c) + (c+a) = a+b+c / (a+a) + (b+b) + (c+c)
= a+b+c / 2a + 2b + 2c = a+b+c / 2(a+b+c) = 1/2 không phải là số nguyên => M không thuộc Z.
Đúng 0
Bình luận (0)
Phan Thanh Tịnh giải sai bét rồi, "+" chứ có phải "-" đâu mà áp dung dãy tỉ số bằng nhau đc
Đúng 0
Bình luận (0)
1. Cho a;b thuộc tập hợp số nguyên. Chứng minh ( a-b ) và ( b-a ) là hai số đối
2. Chứng tỏ rằng:
a, (x-y) + (m-n) = (x+m) - (y+n)
b, (x-y) - (m-n) = (x+n) - (y+m)
1. ta có: (a-b) + (b-a) = a-b+b-a = 0
Vậy (a-b) và (b-a) là hai số đối nhau
2.
a, (x-y) + (m-n) = x-y +m - n = x + m - y - n = (x+m) - (y+n)
b, (x-y) - (m-n) = x-y -m +n = x+n -y -m = (x+n) -(y+m)
Đúng 0
Bình luận (0)
Gọi A = a - b và B = b - a, ta có :
A + B = a - b + b - a
A + B= a + (-b) + b + (-a)
A + B= a + (-a) + b + (-b)
A + B = 0
Vì A + B = 0 mà hai số đối có tổng = 0 nên a - b và b - a là hai số đối nhau.
a) (x - y) + (m - n)= x - y + m - n
= x + (-y) + m + (-n)
= (x + m) + (-y) + (-n)
= (x + m) +[- (y + n)]
= (x + m) - (y + n)
b) (x - y) - (m - n)= x - y - m + n
= x + (-y) + (-m) + n
= (x + n) + (-y) + (-m)
= (x + n) + [- (y + m)]
= (x + n) - (y + m)
Đúng 0
Bình luận (0)
Gọi A = a - b và B = b - a, ta có :
A + B = a - b + b - a
A + B= a + (-b) + b + (-a)
A + B= a + (-a) + b + (-b)
A + B = 0
Vì A + B = 0 mà hai số đối có tổng = 0 nên a - b và b - a là hai số đối nhau.
a) (x - y) + (m - n)= x - y + m - n
= x + (-y) + m + (-n)
= (x + m) + (-y) + (-n)
= (x + m) +[- (y + n)]
= (x + m) - (y + n)
b) (x - y) - (m - n)= x - y - m + n
= x + (-y) + (-m) + n
= (x + n) + (-y) + (-m)
= (x + n) + [- (y + m)]
= (x + n) - (y + m)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho M=a-b+c+1, N=a+2 với a, b, c thuộc Z biết M=N. Chứng tỏ rằng: b và c là 2 số nguyên liền nhau.
Có M=N
=>a-b+c+1=a+2
=>-b+c+1=a+2-a
=>-b+c+1=2
=> c-b=1
Hai số nguyên liền nhau là 2 số có khoảng cách bằng 1
=> c,b là hai số nguyên liền nhau.
Học tốt =P
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b > 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b > a + m b + m
Ta có: 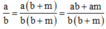
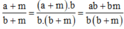
Ta có: a/b > 1 nên a > b suy ra am > bm, suy ra ab + am > ab + bm.
Do đó 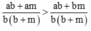
Hay 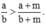
Đúng 0
Bình luận (0)
Cho phân số a/b (a, b ∈ N, b # 0)
Giả sử a b < 1 và m ∈ N, m ≠ 0. Chứng tỏ rằng:
a b < a + m b + m
Cho 3 số a, b, c, dương. M = \(\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}\) . Chứng tỏ rằng M không là số nguyên
Lời giải:
Với $a,b,c>0$ ta có:
$M> \frac{a}{a+b+c}+\frac{b}{b+c+a}+\frac{c}{c+a+b}=\frac{a+b+c}{a+b+c}{a+b+c}=1(*)$
Mặt khác:
Xét hiệu: $\frac{a}{a+b}-\frac{a+c}{a+b+c}=\frac{-bc}{(a+b)(a+b+c)}<0$ với mọi $a,b,c>0$
$\Rightarrow \frac{a}{a+b}< \frac{a+c}{a+b+c}$
Tương tự ta cũng có: $\frac{b}{b+c}< \frac{b+a}{a+b+c}; \frac{c}{c+a}< \frac{c+b}{a+b+c}$
Cộng lại ta được: $M< \frac{a+c+b+a+c+b}{a+b+c}=\frac{2(a+b+c)}{a+b+c}=2(**)$
Từ $(*); (**)\Rightarrow 1< M< 2$ nên $M$ không là số nguyên.
Đúng 1
Bình luận (0)
a) Cho phân số
a
b
(
a
,
b
∈
ℕ
,
b
≠
0
)
.Giả sử
a
b
1 và
m
∈
ℕ
,
m
≠
0
. Chứng tỏ rằng
a
b
a
+
m
b
+
m
.b) Áp dụng so sánh:
437
564...
Đọc tiếp
a) Cho phân số a b ( a , b ∈ ℕ , b ≠ 0 ) .Giả sử a b <1 và m ∈ ℕ , m ≠ 0 . Chứng tỏ rằng a b < a + m b + m .
b) Áp dụng so sánh: 437 564 v à 446 573 .
a) Thực hiện quy đồng a b = a ( b + m ) b ( b + m ) = a b + a m b 2 + b m ;
a + m b + m = b ( a + m ) b ( b + m ) = a b + b m b 2 + b m . Vì a b < 1=> a < b => ab +am < ab + bm
Từ đó thu được a b < a + m b + m
b) 437 564 < 437 + 9 564 + 9 = 446 573 .
Đúng 0
Bình luận (0)
Cho M = (-a b) - (b c-a) + (c-a) trong đó b,c thuộc Z còn a là số nguyên âm . Chứng tỏ rằng M luôn nguyên dương
Đề có vẻ sai nhé bạn!!!
Thiếu dấu!!
hok tốt!!!
^^