1,Chứng tỏ rằng 2110 – 1 chia hết cho 200
H24
Những câu hỏi liên quan
Chứng tỏ rằng 21 10 – 1 chia hết cho 200
* Áp dụng hằng đẳng thức:
![]()
Ta có:
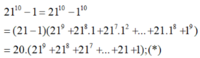
Ta có:
![]()
![]()
gồm có 10 số hạng
![]()
có chữ số tận cùng bằng 0. Do đó, ta có thể viết:
![]()
Thay vào (*) ta được:
2110 - 1 = 20.10.A = 200A
Suy ra: 2110 - 1 chia hết cho 200.
Đúng 0
Bình luận (0)
Chứng minh rằng
a) 2110−1chia hết cho 200
b) 3930+3913chia hết cho 40
c) 260+530chia hết cho 41
link tham khảo
ccaau hỏi của ng duy mạnh
link : https://olm.vn/hoi-dap/detail/60197622644.html
hok tót
Đúng 0
Bình luận (0)
Chứng tỏ rằng 2110 -1 chia hết cho 200
nếu bạn là hs chuyên toán thì mình giải theo cách này
ta thấy 200=8.25 (phân tích thừa số nguyên tố)
ta cần chứng minh 2110-1 đông dư 0 (mod8) ta co 212 đồng dư 1 (mod 8) <=> 2110-1 đồng dư o mod 8 (1)
2110-1 dong du 0 (mod 25) ta có 215 đồng dư 1 (mod 25) <=> 2110-1 đồng dư 0 mod 25 (2)
từ (1) và (2)
tao suy ra..............
Đúng 0
Bình luận (0)
Chứng tỏ rằng biểu thức sau chia hết cho 10:
a)A=(11^200)-1 b)B=(12^300)-(2^300)
a. ta có \(11\equiv1mod10\Rightarrow11^{200}\equiv1mod10\)
nên \(11^{200}-1\equiv0mod10\). Vậy \(11^{200}-1\) chia hết cho 10.
b. ta có \(12\equiv2mod10\Rightarrow12^{200}\equiv2^{200}mod10\)
nên \(12^{200}-2^{200}\equiv0mod10\). Vậy \(12^{200}-2^{200}\) chia hết cho 10.
Chứng tỏ rằng biểu thức sau chia hết cho 10:
a)A=(11^200)-1 b)B=(12^300)-(2^300)
Sorry Nha Toán lớp 6
5) Chứng tỏ 21^10-1 chia hết cho 200
\(21^2\equiv1\left(mod8\right)\Leftrightarrow21^{10}\equiv1^5=1\left(mod8\right)\\ \Leftrightarrow21^{10}-1\equiv0\left(mod8\right)\\ \Leftrightarrow21^{10}-1⋮8\left(1\right)\\ 21^5\equiv1\left(mod25\right)\Leftrightarrow21^{10}\equiv1^2=1\left(mod25\right)\\ \Leftrightarrow21^{10}-1\equiv0\left(mod25\right)\\ \Leftrightarrow21^{10}-1⋮25\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow21^{10}-1⋮25\cdot8=200\)
Đúng 0
Bình luận (0)
chứng minh
A = 1+3+3^2+3^3+...3^11 chứng tỏ rằng chia hết cho 13
B = 3+4+2^2+2^3+....+2^30 chứng tỏ rằng chia hết cho 11
C = 3^1000-1 chứng tỏ rằng chia hết cho 4
TA CÓ:
A=30+3+32+33+........+311
(30+3+32+33)+....+(38+39+310+311)
3(0+1+3+32)+......+38(0+1+3+32)
3.13+....+38.13 cHIA HẾT CHO 13 NÊN A CHIA HẾT CHO 13( đpcm)
Đúng 1
Bình luận (0)
câu a: chứng tỏ rằng n2 + n + 1 không chia hết cho 2
câu b: chứng tỏ rằng n.(n+1) .(5n+1) chia hết cho 6
a)Nếu n=2k(kEN)
thì n2+n+1=4k^2+2k+1(ko chia hết cho 2, vì 1 ko chia hết cho 2)
Nếu n=2k+1(kEN)
thì n2+n+1=n(n+1)+1=(2k+1)(2k+1+1)+1=(2k+1)(2k+2)+1=(2k)(2k+2)+2k+2+1=4k^2+4k+2k+2+1=4k^2+6k+3(ko chia hết cho 2 vì 3 ko chia hết cho 2)
Vậy với mọi nEN thì n2+n+1 ko chia hết cho 2
b)n(n+1)(5n+1)=(n2+n)(5n+1)=5n3+n2+5n2+n
Nếu n=2k(kEN )
thì n(n+1)(5n+1)=10k3+2k2+10k2+2k(chia hết cho 2)
Nếu n=2k+1(kEN)
thì n(n+1)(5n+1)=5(2k+1)3+(2k+1)+5(2k+1)2+2k+1=...................................
tương tự, n=3k;3k+1;3k+2
mỏi tay chết đi được, mấy con số còn bay đi lung tung
Đúng 0
Bình luận (0)
chứng minh \(2^{2^{2n+1}}\)+2110 chia hết cho 7


