Tìm số tự nhiên n để biểu thức là số chính phương:
n4 + 2n3 + 2n2 + 2n + 7
H24
Những câu hỏi liên quan
1.Tìm n ∈ Z để n4+2n3+2n2+n+7 là số chính phương
2.Có tồn tại hay không số có dạng 202020202020…⋮ 2021
Lỡ có sai sót thì thông cảm giúp mình nha:3
Đúng 1
Bình luận (0)
Tìm số tự nhiên n để biểu thức sau là số chính phương
n^2+2n+18
Tìm số tự nhiên n để phân thức N = n 4 - 2 n 3 + 5 n - 2 có giá trị là số nguyên
Điều kiện xác định của phân thức: n ≠ 2
Ta có:
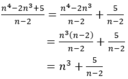
Vậy để N nguyên thì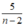 
nguyên ⇒ n – 2 là ước của 5;
Ư
(
5
)
=
-
1
;
1
;
-
5
;
5
n - 2= -1 ⇒ n =1;
n – 2 = 1 ⇒ n =3;
n – 2 = -5 ⇒ n = - 3;
n – 2 = 5 ⇒ n = 7;
vì n ∈ N nên n = 1; n = 3; n = 7
Vậy với n ∈ { 1; 3; 7} thì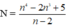 
có giá trị là số nguyên
Đúng 0
Bình luận (0)
tìm số tự nhiên n để 2n3+29 chia hết cho n+7
tìm các số tự nhiên n để giá trị ủa biểu thức A= ( 2n-3 ): (n-9) là 1 số tự nhiên
tìm các số tự nhiên n để biểu thức A =15/2n+1 có giá trị là một số tự nhiên
để A là 1 số tự nhiên thì 2n+1 phải là các ước của 15. Ư(15) \(\in\){ 1; 3; 5; 15}.
2n+1=1 => 2n=0 => n=02n+1=3 => 2n=2 => n=12n+1=5 => 2n=4 => n=22n+1=15 => 2n=14 => n=7
Đúng 0
Bình luận (0)
Tìm các số tự nhiên n để biểu thức A=15/2n+1 có giá trị là 1 số tự nhiên
Để A là số tự nhiên thì 15 chia hết cho 2n+1
\(\Rightarrow\)2n+1\(\inƯ\left(15\right)\)
\(\Rightarrow\)2n+1\(\in\){1,-1,-3,3,5,-5,15,-15}
\(\Rightarrow\)2n\(\in\){0,-2,-4,2,4,-6,14,-16}
\(\Rightarrow\)n\(\in\){0,-1,-2,1,2,-3,7,-8}
Đúng 0
Bình luận (0)
NM
14 tháng 3 2022 lúc 23:08
Cho A = \(\dfrac{n+10}{2n-8}\) - tìm các số nguyên n để biểu thức A có giá trị là phân số .
- tìm các số tự nhiên n để biểu thức A có giá trị là một số nguyên .
A,tìm số tự nhiên n có 2 chữ số để 3n+1 và 4n+1 là số chính phương
B,tìm số tự nhiên n có 2 chữ số để n+4 và 2n là số chính phương