Cho ba đường tròn (O1:5): (O2;7); (O3;9) đôi một tiếp xúc ngoài với nhau.Tiếp điểm của (O1) và (O2) là M. Vẽ O3H vuông góc với O1O2.Tiếp tuyến chung của (O1) và (O2) tại M cắt (O3) tại N và P. Tính NP
PS
Những câu hỏi liên quan
Cho H,K là giao điểm của hai đường tròn tâm O1 và O2.Đường thẳng O1H cắt đường tròn O1 tại A và đường tròn tâm O2 tại B.Đường thẳng O2H cắt đường tròn tâm O1 tại C và đường tròn tâm O2 tại D.Chứng minh:
a, Ba đường thẳng AC,BD,HK đồng quy tại một điểm
b, BH.BA=CH.CD
Cho hai đường tròn O1 và O2 cắt nhau tại 2 điểm A và B. Trêb tia đối tia BA lấy M, từ M kẻ 2 tiếp tuyến ME và MF với đường tròn O1 ( F nằm phía O2 với bờ là đường thẳng AB) . BE và BF cắt đường tròn O2 tại N và Q. Gọi I là giao điểm của NQ và EF. CMR:
a, t/g AFIQ nội tiếp
b, EA.EF=EB.FA
c, IN=IQ
Cho tam giác ABC vuông tại a . Vẽ nửa đường tròn O1 đường kính AB. Nửa đường tròn O2 đường kính AC.Một đường thẳng D quay quanh A cắt đường tròn O1 tại D , O2 tại E.
CMR
Trung điểm DE luôn thuộc đường tròn cố định
Xác định vị trí đường tròn DE sao cho SBDEC lớn nhất
Cho 2 đường tròn (O1),(O2) tiếp xúc ngoài tại A và một đường thẳng tiếp xúc (O1),(O2) lần lượt tại B và C.
a) chứng minh tam giác ABC vuông
b) Gọi M là trung điểm BC. Chứng minh AM là tiếp tuyến chung của (O1),(O2)
c) Chứng minh \(O_1M\perp O_2M\)
d) Các tia BA, CA cắt (O2),(O1) lần lượt tại D và E. Chứng minh diện tích tam giác ADE bằng diện tích tam giác ABC

( Mình sẽ làm tắt nha bạn, mấy chỗ đấy nó dễ rùi nếu ko hiểu thì cmt nhé )
a) Ta có: \(O_1B//O_2C\)( cùng vuông góc với BC )
\(\Rightarrow\widehat{BO_1A}+\widehat{CO_2A}=180^0\)
\(\Leftrightarrow\left(180^0-2\widehat{BAO_1}\right)+\left(180^0-2\widehat{CAO_2}\right)=180^0\)
\(\Leftrightarrow2\left(\widehat{BAO_1}+\widehat{CAO_2}\right)=180^0\)
\(\Leftrightarrow\widehat{BAO_1}+\widehat{CAO_2}=90^0\)
\(\Rightarrow\widehat{BAC}=90^0\)
=> tam giác ABC vuông tại A
b) \(\widehat{O_1BA}+\widehat{MBA}=\widehat{O_1AB}+\widehat{BAM}=90^0\)
\(\Rightarrow\widehat{O_1AM}=90^0\)
\(\Rightarrow AM\perp AO_1\)
=> AM là tiếp tuyến của \(\left(O_1\right)\)
CMTT : AM là tiếp tuyến của \(\left(O_2\right)\)
=> AM là tiếp tuyến chung của \(\left(O_1\right);\left(O_2\right)\)
+) Ta có: \(\hept{\begin{cases}\widehat{BMO_1}=\widehat{AMO_1}\\\widehat{CMO_2}=\widehat{AMO_2}\end{cases}}\)
Ta có; \(\widehat{BMO_1}+\widehat{AMO_1}+\widehat{CMO_2}+\widehat{AMO_2}=180^0\)
\(\Leftrightarrow2\left(\widehat{O_1AM}+\widehat{AMO_2}\right)=180^0\)
\(\Leftrightarrow\widehat{O_1AM}+\widehat{AMO_2}=90^0\)
\(\Leftrightarrow\widehat{O_1MO_2}=90^0\)
\(\Rightarrow O_1M\perp O_2M\)
d) Ta có: \(\widehat{O_1BA}=\widehat{O_1AB}=\widehat{O_2AD}=\widehat{O_2DA}\)
\(\widehat{\Rightarrow O_1BA}=\widehat{O_2DA}\)mà 2 góc này ở vị trí so le trong
\(\Rightarrow O_1B//O_2D\)
\(\Rightarrow\frac{AB}{AD}=\frac{AO_1}{AO_2}\left(1\right)\)
CMTT \(\Rightarrow\frac{AE}{AC}=\frac{AO_1}{AO_2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{AB}{AD}=\frac{AE}{AC}\)
\(\Rightarrow AB.AC=AD.AE\)
\(\Rightarrow\frac{1}{2}AB.AC=\frac{1}{2}AD.AE\)
\(\Rightarrow S_{\Delta ADE}=S_{\Delta ABC}\)
Một khối trụ tròn có thể tích là V, các đường tròn đáy có tâm là
O
1
,
O
2
(hình vẽ). Xét hình nón
N
1
đỉnh
O
1
, đáy là đường tròn đáy tâm
O
2
của hình trụ, hình nón
N
2
đỉnh
O
2
, đáy là đ...
Đọc tiếp
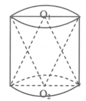
Một khối trụ tròn có thể tích là V, các đường tròn đáy có tâm là O 1 , O 2 (hình vẽ). Xét hình nón N 1 đỉnh O 1 , đáy là đường tròn đáy tâm O 2 của hình trụ, hình nón N 2 đỉnh O 2 , đáy là đường tròn đáy tâm O 1 của hình trụ. Gọi V O là phần thể tích chung của N 1 , N 2 . Tính k = V O V
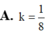
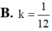
![]()
![]()
Cho nửa đường tròn (O) đường kính AB. Lấy M là điểm tuỳ ý trên nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB (H
∈
AB). Trên cùng nửa mặt phang bờ AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm
O
1
, đường kính AH và tâm
O
2
, đường kính BH. Đoạn MA và MB cắt hai nửa đường tròn (
O
1
) và...
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB. Lấy M là điểm tuỳ ý trên nửa đường tròn (M khác A và B). Kẻ MH vuông góc với AB (H ∈ AB). Trên cùng nửa mặt phang bờ AB chứa nửa đường tròn (O) vẽ hai nửa đường tròn tâm O 1 , đường kính AH và tâm O 2 , đường kính BH. Đoạn MA và MB cắt hai nửa đường tròn ( O 1 ) và ( O 2 ) lần lượt tại P và Q. Chứng minh:
a, MH = PQ
b, Các tam giác MPQ và MBA đồng dạng
c, PQ là tiếp tuyến chung của hai đường tròn ( O 1 ) và ( O 2 )
a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c, P M H ^ = M B H ^ => P Q H ^ = O 2 Q B ^ => PQ là tiếp tuyến của O 2
Tương tự PQ cũng là tiếp tuyến ( O 1 )
Đúng 0
Bình luận (0)
Cho hai đường tròn ( O1 ) và ( O2 ) ngoài nhau. Gọi AB là một tiếp tuyến chung ngoài và CD là một tiếp tuyến chung trong của hai đường tròn ( A, C ϵ ( O1 ) ; ( B, D ϵ ( O2 ). Chứng minh AC, BD, O1O2 đồng quy
Bài 2 : Cho 3 đường tròn O1,O2,O3 đôi một tiếp xúc với nhau ở A,B,C.A thuộc (O1) và (O2), B thuộc (O2) và (O3), C thuộc (O1) và (O3).E là giao của AC và (O3). F là giao của AB và (O3).CMR: 3 điểm E;F;tâm của đường tròn O3 thẳng hàng!!
Giúp mình nhé các bạn
Nối O1O2; O2O3; O1O3. Đây là các đường nối tâm của hai vòng tròn tiếp xúc nhau
=> O1; C; O3 thẳng hàng, O1; A; O2 thẳng hàng và O2; B; O3 thẳng hàng
Nối E với O3 và F với O3
Xét tam giác O1AC có O1A=O1C (bk đường tròn (O1)) => tg O1AC cân tại O1 => ^O1AC=^O1CA (1)
Xét tam giác O3CE có O3C=O3E (bk đường tròn (O3)) => tg O3CE cân tại O3 => ^O3CE=^O3EC (2)
Mà ^O1CA=^O3CE (góc đối đỉnh) (3)
Từ (1) (2) và (3) => ^O1AC=^O3EC => O1O2//O3E (*)
Tương tự như thế ta cũng c/m được O1O2//O3F (**)
Từ (*) và (**) => E; F; O3 thảng hàng (Từ O3 chỉ dựng được duy nhất 1 đường thẳng // O1O2)
o ba đường tròn (o),(o1),(o2) có bán kình r,r1,r2 tiếp xúc ngoài đôi một. tìm độ dài dây ab mà tiếp tuyến chung ngoài cua (0) và (o1) cắt (02) theo r,r1,r2
Cho 2 đường tròn (O1), (O2) cắt nhau tại A và B. Tiếp tuyến của (O2) tại A cắt (O1) tại C và tiếp tuyến tại B của (O1) cắt (O2) tại D. Chứng minh:
a) AD song song với BC.
b) AB2 = AD . BC
c) \(\dfrac{BD^2}{AC^2}=\dfrac{AD}{BC}\)


