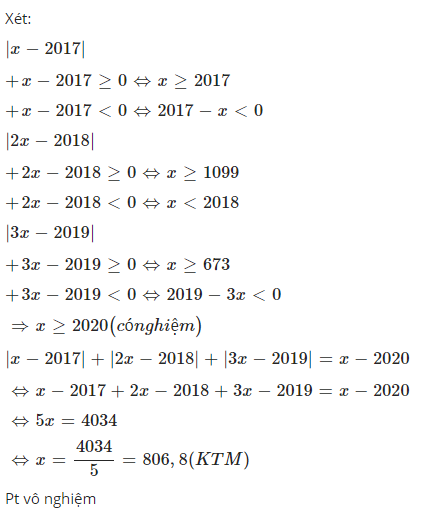(3x-7)^2019=(3x-7)^2017
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
DT
Những câu hỏi liên quan
Tìm x biết:(3x-5)^2017=(3x-5)^2019
tìm x biết: (3x-7)2015=(3x-7)2017
\(\left(3x-7\right)^{2015}=\left(3x-7\right)^{2017}\Rightarrow\left(3x-7\right)^{2017}-\left(3x-7\right)^{2015}=0\Leftrightarrow\left(3x-7\right)^{2015}\left[\left(3x-7\right)^2-1\right]=0\Leftrightarrow\orbr{\begin{cases}3x-7=0\\\left(3x-7\right)^2=1\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}3x=7\\3x-7=1\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{7}{3}\\x=\frac{1+7}{3}=\frac{8}{3}\end{cases}}\)
Vậy phương trình có hai nghiệm là \(x=\frac{7}{3}\)và \(x=\frac{8}{3}\)
Đúng 0
Bình luận (0)
Vì \(\left(3x-7\right)^{2015}=\left(3x-7\right)^{2017}\) =>3x-7=0 hoặc 3x-7=1
Nếu 3x-7=0=>x=\(\frac{7}{3}\)Nếu 3x-7=1=>x=\(\frac{8}{3}\)Vậy \(x=\orbr{\begin{cases}\frac{7}{3}\\\frac{8}{3}\end{cases}}\)
Đúng 0
Bình luận (0)
(-3x-15)2017(-20172016^2018^2019-20192018^-
2017^2016)=0
Tìm giá trị nhỏ nhất của
P=|x+3|+|2x-5|+|x+7|
Q=|x+1|+|3x-a|+|x-1|+5
M=|x+2017|+|x-2018|+|x-2019|
Ai nhanh mình tick
Giải phương trình: \(|x-2017|+|2x-2018|+|3x-2019|=x-2020\)
Nhận thấy vế trái luôn dương nên \(x-2020\ge0\Leftrightarrow x\ge2020\)
Với \(x\ge2020\Rightarrow\left\{{}\begin{matrix}x-2017\ge0\\2x-2018\ge0\\3x-2019\ge0\end{matrix}\right.\)
PT trở thành: \(x-2017+2x-2018+3x-2019=x-2020\)
Hay kết hợp với điều kiện \(x=\dfrac{4034}{5}\) suy ra PT đã cho vô nghiệm
Đúng 2
Bình luận (2)
\(\left|x-2017\right|+\left|2x-2018\right|+\left|3x-2019\right|=x-2020\)
\(ĐK:x\ge2020\)
\(\Leftrightarrow x-2017+2x-2018+3x-2019=x-2020\)
\(\Leftrightarrow5x=4034\)
\(\Leftrightarrow x=806,8\left(tm\right)\)
Vậy \(S=\left\{806,8\right\}\)
Đúng 0
Bình luận (2)
Tìm x, biết: \(\left(3x-7\right)^{2015}\)=\(\left(3x-7\right)^{2017}\)
(3x - 7)2015 = (3x - 7)2017
(3x - 7)2017 - (3x - 7)2015 = 0
(3x - 7)2017[(3x - 7)2 - 1] = 0
=> (3x - 7)2017 = 0 hoặc (3x - 7)2 = 1
=> 3x - 7 = 0 hoặc 3x - 7 = ± 1
=> x = 7/3 hoặc x = { 8/3 ; 2 }
Vậy x = { 2; 7/3; 8/3 }
Đúng 0
Bình luận (0)
\(y\left(y^2-1\right)=0\Leftrightarrow\orbr{\begin{cases}y=0\\y^2-1=0\end{cases}}\)
Đúng 0
Bình luận (0)
(3x - 7)^2015 = (3x - 7)^2017
(3x - 7)^2017 - (3x - 7)^2015 = 0
(3x - 7)^2017 [(3x - 7)^2 - 1] = 0
=> (3x - 7)^2017 = 0 hoặc (3x - 7)^2 = 1
=> 3x - 7 = 0 hoặc 3x - 7 = ± 1
=> x = 7/3 hoặc x = { 8/3 ; 2 }
Vậy x = { 2; 7/3; 8/3 }
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1. 2019/2020-(2019/2020-2020/2021)
2.2/9+7/9 :(42/5-7/5
3.a)3/4+x/4=5/8
4./3x+1/-1/4=-1/4
1. \(\dfrac{2019}{2020}-\left(\dfrac{2019}{2020}-\dfrac{2020}{2021}\right)\)
\(=\dfrac{2019}{2020}-\dfrac{2019}{2020}+\dfrac{2020}{2021}\)
\(=0+\dfrac{2020}{2021}=\dfrac{2020}{2021}\)
Đúng 2
Bình luận (0)
Giải:
1) \(\dfrac{2019}{2020}-\left(\dfrac{2019}{2020}-\dfrac{2020}{2021}\right)\)
\(=\dfrac{2019}{2020}-\dfrac{2019}{2020}+\dfrac{2020}{2021}\)
\(=\left(\dfrac{2019}{2020}-\dfrac{2019}{2020}\right)+\dfrac{2020}{2021}\)
\(=0+\dfrac{2020}{2021}\)
\(=\dfrac{2020}{2021}\)
2) \(\dfrac{2}{9}+\dfrac{7}{9}:\left(\dfrac{42}{5}-\dfrac{7}{5}\right)\)
\(=\dfrac{2}{9}+\dfrac{7}{9}:7\)
\(=\dfrac{2}{9}+\dfrac{1}{9}\)
\(=\dfrac{1}{3}\)
3) \(\dfrac{3}{4}+\dfrac{x}{4}=\dfrac{5}{8}\)
\(\dfrac{x}{4}=\dfrac{5}{8}-\dfrac{3}{4}\)
\(\dfrac{x}{4}=\dfrac{-1}{8}\)
\(\Rightarrow x=\dfrac{4.-1}{8}=\dfrac{-1}{2}\)
4) \(\left|3x+1\right|-\dfrac{1}{4}=\dfrac{-1}{4}\)
\(\left|3x-1\right|=\dfrac{-1}{4}+\dfrac{1}{4}\)
\(\left|3x-1\right|=0\)
\(3x-1=0\)
\(3x=0+1\)
\(3x=1\)
\(x=1:3\)
\(x=\dfrac{1}{3}\)
Chúc bạn học tốt!
Đúng 2
Bình luận (4)
4) \(\left|3x+1\right|-\dfrac{1}{4}=\dfrac{-1}{4}\)
\(\left|3x+1\right|=\dfrac{-1}{4}+\dfrac{1}{4}\)
\(\left|3x+1\right|=0\)
\(3x+1=0\)
\(3x=0-1\)
\(3x=-1\)
\(x=-1:3\)
\(x=\dfrac{-1}{3}\)
Đúng 1
Bình luận (0)
Giải phương trình: |x-2017|+|2x-2018|+|3x-2019|=x-2020
2x(3x-7)(6x+5)(x-3)-2019=0
Tìm x nha